Seja parte do plano limitada pelos planos , e . Calcule
Onde com
Passo 1
A questão pede para a gente calcular uma integral de superfície, né? Vamos então seguir o passo a passo de sempre, precisamos encontrar uma parametrização para a nossa superfície, depois achar o vetor normal à ela e depois substituir tudo na integral, vamos lá?
Vamos primeiro então parametrizar nossa superfície. Como ela é um plano, o jeito mais fácil de parametrizar é da forma explícita, nesse caso vamos explicitar em para evitar denominadores, fica assim:
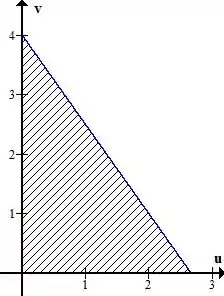
Os limites do plano são:
Passo 2
Agora que temos a parametrização, vamos pensar na reta normal ao plano. Tem dois jeitos da gente fazer isso aqui: o primeiro é aquele jeito que fazemos para qualquer superfície, que precisamos derivar em relação a e a e fazer o produto vetorial desses dois termos, assim:
Ou podemos lembrar que, a normal do plano é exatamente os termos que estão multiplicando , e na sua equação! Ou seja, como nossa equação é , sua normal vai ser porque está multiplicado por , por e por .
Só para checar o sentido da normal, o enunciado diz que , lembrando que
Então estamos usando a normal correta!
Passo 3
Definidas a parametrização e a normal, vamos voltar para a nossa integral:
Passo 4
Pronto, agora é só resolver!
Vamos colocar esse termo que está aparecendo três vezes ao quadrado em evidência:
Fazendo o MMC nos denominadores (o primeiro é igual a e o segundo é igual a )
Vamos tentar simplificar essa integral fazendo uma mudança de variável, vamos chamar esse termo de :
Então nossa integral fica: