23) Calcule
f) e é a semiesfera , , com exterior.
Passo 1
Sabemos que o fluxo de um campo sobre uma superfície é dado por uma integral de superfície dessa forma aqui:
Mas se você notar bem, a superfície se você a desenhar, vai reparar que se trata da metade da esfera:
Como o divergente desse campo é mole:
Como
Resolver pelo Teorema de Gauss vai ser uma maravilha! 😊
Passo 2
Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:
1º - Uma superfície fechada delimitando o sólido .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 3
Quanto ao primeiro quesito, ter uma superfície fechada, já falhamos. Afinal de contas a nossa superfície é uma superfície aberta na parte de cima em :
Ora! Se a superfície só não é fechada por um círculosinho em cima do plano , fechamos esse cara com essa tampa!
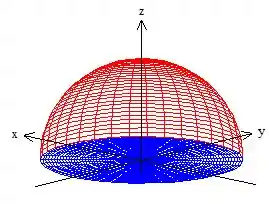
A essa superfície que acabamos de adicionar, daremos um nome de , mas não se preocupe, é apenas um nome ok? E veja também que essa superfície tem o raio igual ao da esfera, ou seja, 😉
Passo 4
2º - Sem singularidades na função Vetorial:
Esse campo Vetorial funciona em todas as situações, afinal ele não tem nenhuma divisão por ou algo do tipo.
3º - Superfície orientada positivamente:
Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado. Então é pra fora que o nosso vetor aponta (orientada positivamente 😉)
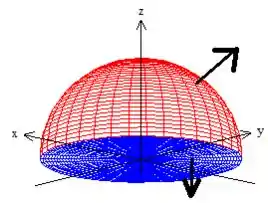
Passo 5
Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...
Aqui só tenho um detalhe que preciso te falar! A integral de superfície do teorema é calculada em cima da superfície que fecha o sólido . E esse cara é
Logo, temos que desmembrar a integral de superfície em duas...
Vamos só fazer mais simplificações aqui... Passando a integral de pro outro lado...
Passo 6
Eu sei que parece loucura trocar o cálculo de uma integral de superfície por outras duas integrais! Mas pode acreditar talvez é o único jeito mesmo ainda mais nesse caso 😐!
Mas vamos começar aqui então pela integral tripla...
Que maravilha 😊! Pois conhecemos o volume da semiesfera de raio ...
Então...
Passo 7
Concluímos uma etapa, mas ainda nos falta encontrar qual é o resultado da integral de superfície de em cima de superfície que adicionamos, ou seja, a tampa onde ...
O vetor por ser um vetor normal unitário apontado pra baixo... Pode ser escrito como...
Logo...
Resolvendo esse produto escalar...
Agora é só calcular essa integral de superfície do caso escalar 😉!
Estamos em cima do plano , logo...
Passo 8
Veja bem, encontramos o valor da integral em . Mas como vimos do teorema de Gauss...
Então