Dados o campo e a superfície fechada que delimita o cilindro
com a normal apontando para fora. Calcule:
(a) O fluxo de através da base de que está contida no plano
Passo 1
Nossa região está com os eixos trocados, não é aquele cilindro normal que a gente geralmente desenha no eixo , olha só como é o esboço desse aqui
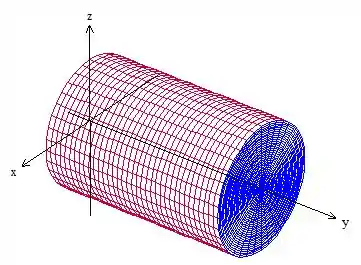
A base desse cilindro no plano nada mais é do o círculo
Esse aqui
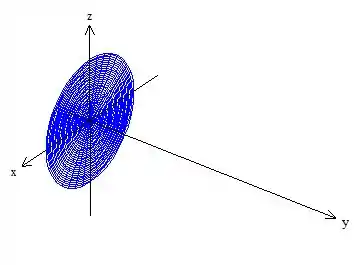
O fluxo de que o enunciado pediu pra gente é calculado pela integral de superfície
Precisamos então parametrizar essa superfície, calcular a normal e calcular a integral, vamos lá?
Passo 2
Começando pela parametrização, como a superfície é um circulo de raio em , podemos fazer isso aqui
Para calcular a normal à superfície, precisamos fazer o produto vetorial entre as derivadas de , assim
Como a normal deve estar apontando para fora no esboço do passo 1, o valor de deve ser negativo, portanto
Antes de colocar tudo na integral, precisamos descobrir como fica escrito com e
Bem complicado né? Vamos ver que fazendo o produto escalar com a normal vai ficar mais simples.
Passo 3
Na integral