Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial

Ver Teoria
Exercício 3312345678910111213141516171819202122232425262728293031323435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

UTFPR. Calculo Avançado. Lista 2 de Exercícios - Cálculo Vetorial. AV1. Questão 2b.

2. Calcule a integral de superfície ∫ ∫ S F . d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação (para fora) positiva.

b) F x , y , z = x z e y i - x z e y j + z k , S é a parte do plano x + y + z = 1 no primeiro octante, com orientação para baixo.

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão, temos uma integral de superfície em seu caso vetorial.

Lembra o que temos que fazer quando aparece esse tipo de problema? 🤔

A ideia é calcular a integral

∫ ∫ S F · N d A

Onde F é a função vetorial parametrizada que é dada no enunciado, N é um vetor normal a S e d A é a área da nossa parametrização.

No caso, nossa função vetorial é dada por F x , y , z = x z e y i - x z e y j + z k e S é a parte do plano x + y + z = 1 que está no primeiro octante, ou seja, onde x , y e z são maiores ou iguais a 0 .

Vamos dar uma olhada na nossa região S ?

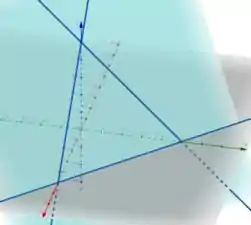
Aproveitando, o que acha de começarmos parametrizando a superfície S ?

Bora lá! 😁

Passo 2

A ideia da parametrização é escrever a superfície de três variáveis por meio de duas variáveis.

Vamos escrever em função de x e y , x continua sendo x e y continua sendo y .

Isolando z , vemos que podemos escreve-lo com

z = 1 - x - y

Com isso, nossa parametrização P x , y é

P x , y = x , y , 1 - x - y

Para obter N , vamos derivar P com relação a x e a y e calcular o produto vetorial entre eles.

Primeiro derivando com relação a x , temos

∂ P ∂ x = ∂ x , y , 1 - x - y ∂ x

Pelo método de derivação polinomial, temos

∂ P ∂ x = x 1 - 1 , 0 y , 0 1 - x 1 - 1 - 0 y

∂ P ∂ x = 1,0 , - 1

Agora derivando P com relação a y

∂ P ∂ y = ∂ x , y , 1 - x - y ∂ y

Aplicando o mesmo método de derivação

∂ P ∂ y = 0 x , y 1 - 1 , 0 1 - 0 x - y 1 - 1

∂ P ∂ y = 0,1 , - 1

Tranquilo até aqui? 👀

Passo 3

Como no enunciado foi dito que a orientação de S é para baixo, vamos calcular o produto vetorial ∂ P ∂ y X ∂ P ∂ x , ou seja

N = ∂ P ∂ y X ∂ P ∂ x = i j k 0 1 - 1 1 0 - 1

Calculando esse determinante, temos

N = - 1 i - 1 j - 1 k

A próxima etapa é calcular o produto interno entre F x , y e N

Mas antes temos que obter F x , y

Aplicando a parametrização em F onde x continua sendo x , y continua sendo y e z se transforma em 1 - x - y

F x , y = x 1 - x - y e y i - x 1 - x - y e y j + z k

Organizando essa função, temos

F x , y = x e y - x 2 e y - y e y i - x e y - x 2 e y - y e y j + 1 - x - y k

Agora sim! Calculando o produto interno F x , y · N .

F x , y · N = - x e y - x 2 e y - y e y - - x e y - x 2 e y - y e y - 1 - x - y

Perceba que o primeiro termo se cancela com o segundo termo, ou seja

F x , y · N = x + y - 1

Como vimos no enunciado, queremos a parte positiva de x , y e z .

Se isolarmos x na equação S , temos

x = 1 - y - z

Como y e z são positivos e fazendo z = 0 , o maior valor para x é 1 - y .

Fazendo o mesmo para y

y = 1 - x - z

Da mesma forma, mas agora fazendo x e z ser 0 , o maior valor possível para y é 1 .

Assim, obtemos os limites de integração como

0 ≤ x ≤ 1 - y 0 ≤ y ≤ 1

Bacana, não é? 😎

Passo 4

Com essas informações que obtemos, podemos definir nossa função de integração como

∫ 0 1 ∫ 0 1 - y x + y - 1 d x d y

Integrando nossa função com relação a x pelo método de integração polinomial, temos

∫ x + y - 1 d x = x 1 + 1 1 + 1 + y x - 1 x

∫ x + y - 1 d x = x 2 2 + y x - x

Aplicando os limites de integração

∫ 0 1 - y x + y - 1 d x = 1 - y 2 2 + y 1 - y - 1 - y - 0 2 2 + y 0 - 0

∫ 0 1 - y x + y - 1 d x = 1 - 2 y + y 2 2 + y - y 2 - 1 - y

Simplificando o resultado, temos

∫ 0 1 - y x + y - 1 d x = - y 2 2 + y - 1 2

Agora integramos o resultado com relação a y pelo mesmo método de integração

∫ - y 2 2 + y - 1 2 d y = - y 2 + 1 2 2 + 1 + y 1 + 1 1 + 1 - 1 2 y

∫ - y 2 2 + y - 1 2 d y = - y 3 6 + y 2 2 - 1 2 y

Aplicando os limites de integração

∫ 0 1 - y 2 2 + y - 1 2 d y = - 1 3 6 + 1 2 2 - 1 2 1 - - 0 3 3 + 0 2 2 - 1 2 0

∫ 0 1 - y 2 2 + y - 1 2 d y = - 1 6

Com isso, mostramos que o fluxo F em S é de - 1 6 !

Fim! Iae, o que achou? Responde Aí! 😁

Resposta

∫ 0 1 ∫ 0 1 - y x + y - 1 d x d y = - 1 6

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua