Calcule a integral de superfície para cada um dos campos de vetores e superfícies orientadas indicadas abaixo. Em outras palavras, calcule o fluxo de através de . Quando é uma superfície fechada, admita que está orientada pela normal exterior.

e é a parte da esfera exterior ao cilindro , orientada de modo que a normal no ponto é ;

Primeiro é interessante visualizarmos a nossa superfície, temos que

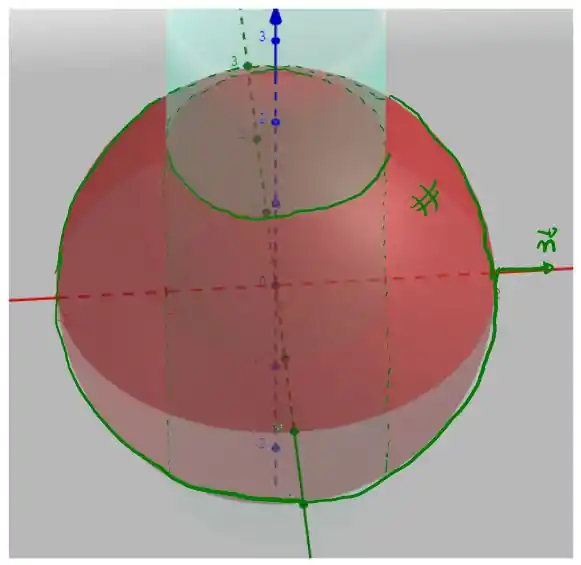
é como se você cavasse um buraco cilindro dentro de uma esfera! A parametrização da esfera pode ser feita utilizando coordenadas esféricas, em que

calculando as derivadas parciais em relação a e , temos que

e, as derivadas parciais em relação a são da forma

Usando a definição matricial de produto vetorial, podemos calcular o produto vetorial entre eles como

Esse é o vetor normal, no ponto , que ocorre quando o ângulo polar e o ângulo , temos que

portanto, este vetor está apontando para dentro da esfera, o que desejamos deve apontar para fora, portanto, vamos utilizar o vetor

Vamos aplicar isso em nossa integral de superfície! Vem comigo!

Primeiro, vamos escrever o nosso campo vetorial nas coordenadas da nossa parametrização, temos que

fazendo o produto escalar com o nosso vetor normal, temos que

a nossa integral é tal que

mas quais são os limites de integração? Os limites de são simplesmente , agora, os limites para podem ser obtidos fazer a interseção do cilindro e da esfera em coordenadas esféricas, temos que

que resulta em

portanto, temos que o ângulo é tal que

Portanto, temos que , como eles se interceptam duas vezes, temos que os limites de são dados por . A integral é então dada por

Vamos começar a resolver agora! Vem comigo!

Aqui é bastante direto, podemos integrar qualquer variável primeiro, começando por , temos que

fazendo a mudança de variáveis

e

obtemos que e , portanto, a nossa integral tem a forma

já que os limites são iguais! Isso resolve a nossa questão, pois temos que

A questão foi isso! Te vejo na próxima! Tchau Tchau!