UFSC, Sem Campus, Cálculo C, Provas Professor Saeger - P2 2019.2, Questão 5b
Seja , sendo , e
b) Esboce a curva C e o campo vetorial integrado no item a) em quatro pontos de C.
Passo 1
Olá meu amigo, tudo bem? Agora é hora de vermos a curva que integramos anteriormente, para isso iremos utilizar o geogebra. Para entender o que iremos fazer aqui é importante que você tenha visto o que fizemos na letra a dessa questão. Mas aqui o que iremos fazer é desenhar o caminho pelo qual calculamos a integral. O que fizemos na questão anterior foi criar duas retas AB e BD, com parametrização
O parâmetro em relação a x
A parametrização em relação a y
Agora para
Aqui estamos apenas desenhando o caminho que elas seguiram. O trecho verde em o caminho e que foi parametrizado pelo enunciado da questão.
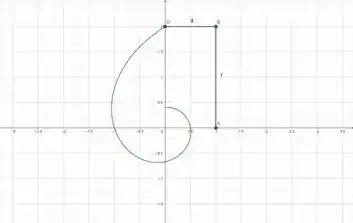
Passo 2
E também com a ajuda do GeoGebra iremos esboçar o campo vetorial. Para esboçar um campo vetorial tudo que a gente precisa fazer é testar alguns pontos e ir desenhando os vetores, até achar o padrão e poder aplicar isso para todos os pontos.
Como ficar fazendo na mão é tedioso mas você meu amigo já aprendeu como faz, deixo aqui o campo gerado pelo GeoGebra.
Resposta
Resposta nos passos