Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial

Ver Teoria
Exercício 3124567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Encontre o fluxo do campo vetorial F através de σ . Onde F x ,   y ,   z = x + y i + y + z j + z + x k ; σ é a porção do plano x + y + z = 1 do primeiro octante, orientada por vetores normais unitários com componentes positivos.

Passo 1

Podemos usar a parametrização explícita para descrever nosso plano, então devemos encontrar z = f ( x , y ) :

x + y + z = 1

z = 1 - x - y  

Assim, a parametrização será:

x = u y = v z = 1 - u - v

φ u , v = ( u ,   v ,   1 - u - v )

Passo 2

Vamos calcular o vetor normal unitário a essa superfície. Para a parametrização explícita sabemos que:

N → u , v = - ∂ f ∂ u u , v ,   - ∂ f ∂ v u , v ,   1

N → u , v = 1,1 , 1

Passo 3

Agora vamos encontrar os intervalos dos parâmetros. Como é a porção do plano no primeiro octante, todas as variáveis são maiores que zero, logo:

u ≥ 0 ,   v ≥ 0

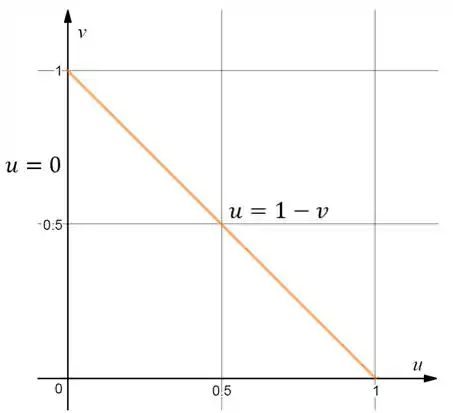
Note que as variáveis x e y variam no triângulo formado pela projeção de σ no plano x y , onde z = 0 :

z = 1 - u - v

0 = 1 - u - v

u = 1 - v

Então para cada v variando entre

0 ≤ v ≤ 1

Teremos que u   vai variar de 0 até 1 - v , que é o limite da reta, assim:

0 ≤ u ≤ 1 - v

Veja a imagem para entender melhor

Passo 4

O cálculo do fluxo é dado por:

∬ σ F . n d S

∬ σ ( u + v , 1 - u , 1 - v ) . 1,1 , 1 d u d v

∫ 0 1 ∫ 0 1 - v 2 d u d v

2 ∫ 0 1 ( 1 - v ) d v = 2 v - v 2 2 0 1 = 1

Assim, o fluxo é

∬ σ F . n d S = 1

Resposta

∬ σ F . n d S = 1

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua