UFF, Niterói - Campus da Praia Vermelha, Cálculo IIIA, P2 - 2022.2, Questão 3
Calcule a área lateral da superfície do solido dado por e
Passo 1
Por simetria, basta calcular área de um dos 4 "lados", e multiplicar por 4. Vamos calcular área do lado "direito":
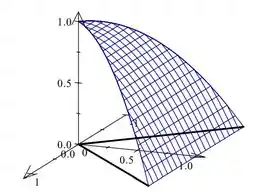
Este lado pode ser parametrizado como gráfico de função:
onde e
Passo 2
Pois a interseção dos dois cilindros é . Assim:
E enfim
Resposta
Exercícios de Livros Relacionados
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua