Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial

Ver Teoria
Exercício 9123456781011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Teorema de Gauss

Calcule ∬ S   F → . N → d S sendo F → x , y , z = x 3 12 , y 3 48 , z e S é parte da superfície x 2 4 + y 2 16 = 1 , limitada pelos planos z = 3 e z = - 3 , orientada pela normal N → que se afasta do eixo z (exterior).

Passo 1

Temos um cilindro de seção elíptica x 2 4 + y 2 16 = 1 cortado pelos planos z = 3 e z = - 3 :

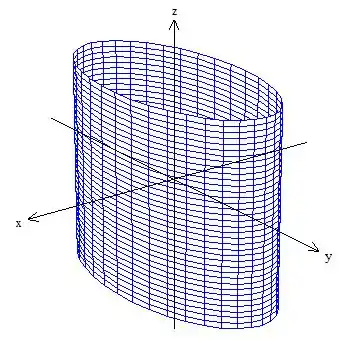
Com normal apontando para fora dele. Queremos ∬ S   F → . N → d S

Passo 2

Certo, agora vamos parametrizar essa superfície. Como se trata de um cilindro, vamos usar coordenadas cilíndricas:

x 2 4 + y 2 16 = 1

x = 2 cos ⁡ θ

y = 4   s e n   θ

z = z

Logo

φ θ , z = 2 cos ⁡ θ , 4   s e n   θ , z

Esses coeficientes na mudança cilíndrica estão aí para cancelar os denominadores da equação do cilindro.

Show, agora vamos ver os intervalos. Como temos uma volta completa em torno do eixo z , temos 0 ≤ θ ≤ 2 π . Como o próprio enunciado diz, - 3 ≤ z ≤ 3 .

Passo 3

Agora, vamos encontrar o vetor normal à superfície:

∂ φ ∂ θ = - 2   s e n   θ , 4 cos ⁡ θ , 0

∂ φ ∂ = ( 0,0 , 1 )

∂ φ ∂ θ × ∂ φ ∂ z = i ^ j ^ k ^ - 2   s e n   θ 4 cos ⁡ θ 0 0 0 1 = 4 cos ⁡ θ , 2   s e n   θ , 0

Como o enunciado diz que a normal está apontando para fora do cilindro, encontramos o vetor correto, você pode testar o ângulo θ = 0 para ver isso, temos 4,0 , 0 .

Passo 4

Beleza, agora vamos levar o que encontramos para a integral:

∬ S   F → . n → d S = ∬ D   F → φ θ , z ∂ φ ∂ θ × ∂ φ ∂ z d θ d z

O campo nas variáveis da parametrização fica

F → φ θ , z = 2 cos ⁡ θ 3 12 , 4   s e n   θ 3 48 , z

∬ S   F → . n → d S = ∬ D   8 12 cos 3 ⁡ θ , 64 48 s e n 3 θ , z 4 cos ⁡ θ , 2   s e n   θ , 0 d θ d z

Onde D = - 3 ≤ z ≤ 3 ,   0 ≤ θ ≤ 2 π .

∬ S   F → . n → d S = ∫ 0 2 π ∫ - 3 3 8 3 cos 4 ⁡ θ + 8 3 s e n 4 θ d z d θ

Passo 5

Agora é só resolver isso aí

= ∫ 0 2 π z 8 3 cos 4 ⁡ θ + 8 3 s e n 4 θ - 3 3 d θ =

= 6 ∫ 0 2 π 8 3 cos 4 ⁡ θ + 8 3 s e n 4 θ d θ =

Agora precisamos usar as relações:

s e n 2 θ = 1 - cos ⁡ 2 θ 2

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

= 16 ∫ 0 2 π 1 + cos ⁡ 2 θ 2 2 + 1 - cos ⁡ 2 θ 2 2 d θ =

= 4 ∫ 0 2 π 1 + 2 cos ⁡ 2 θ + cos 2 ⁡ 2 θ + 1 - 2 cos ⁡ 2 θ + cos 2 ⁡ 2 θ d θ =

= 8 ∫ 0 2 π 1 + cos 2 ⁡ 2 θ d θ =

Usando aquela relação de novo, temos:

= 8 ∫ 0 2 π 1 + 1 + cos ⁡ 4 θ 2 d θ =

= 4 ∫ 0 2 π 3 + cos ⁡ 4 θ d θ =

= 4 θ 3 + 1 4 s e n 4 θ 0 2 π =

= 24 π

Resposta

24 π

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua