USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 5j
Calcule a integral de superfície para cada um dos campos de vetores e superfícies orientadas indicadas abaixo. Em outras palavras, calcule o fluxo de através de . Quando é uma superfície fechada, admita que está orientada pela normal exterior.
e é a parte da superfície limitada pela superfície cilíndrica , orientado de modo que a sua normal satisfaz ;
Passo 1
Eaew, belezinha?
Nós temos que calcular a seguinte integral de superfície
para esta alternativa, temos o seguinte campo vetorial
e a nossa superfície é a parte da superfície limitada pela superfície cilíndrica , e orientada de forma que . Vamos tentar utilizar a seguinte definição para resolver o nosso problema
em que temos uma parametrização de nossa superfície! Bora lá!
Passo 2
Primeiro é interessante visualizarmos a nossa superfície, temos que
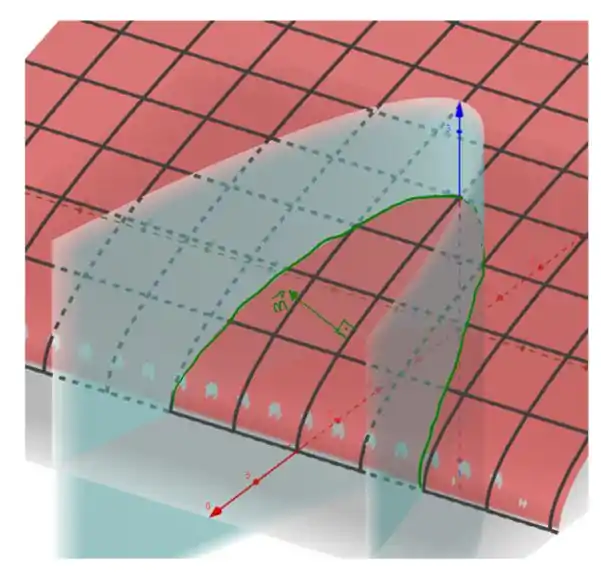
precisamos parametrizar essa superfície da seguinte maneira
portanto, as derivadas parciais são da forma
para a derivada em , temos que
se fizermos o produto vetorial, podemos obter o seguinte vetor normal
em que o fiz o produto vetorial usando a definição através do determinante, note que temos que , portanto, podemos usar esse vetor sem problemas! Vamos continuar com o nosso problema agora!
Passo 3
Escrevendo o campo vetorial usando a nossa parametrização, temos que
e, portanto, o produto escalar em nosso integrando se torna
A integral se torna
observando a nossa figura, temos que e que . A nossa integral se torna então
Vamos calcular as integrais agora! Bora lá!
Passo 4
Vamos começar com as integrações em , temos que
a primeira pode ser obtida como
pois temos uma função ímpar em intervalos simétricos, agora para a outra integral em , temos que
A nossa integral se reduz agora à
Vamos resolver as integrais que faltam agora! Vem comigo!
Passo 5
Temos que
A nossa integral pode ser finalmente ser obtida como
A questão foi isso! Te vejo na próxima! Tchau Tchau!