Considere todos os triângulos retângulos cujos catetos estão contidos nos eixos coordenadas e que a hipotenusa contém o ponto (3,2). A menor área que um desses triângulos pode ter é quanto?
Passo 1
E aí, galerinha! Tudo na paz por aí?
Tu se lembra o que é um triângulo retângulo? É aquele que faz 90° em algum lugar dos vértices, o clássico triângulo de Pitágoras. Esse aí que desenhei !!
Bem, imagine que ali na hipotenuse, um ponto que você tem certeza que faz parte dele é (3,2). E como é uma reta, a hipotenusa vai ter uma expressão com a carinha , certo?
Agora que sabemos a cara da reta e o ponto pertencente à esta reta, vem comigoooo que te mostro o caminho!
Passo 2
A reta que passa pelos ponto e , com , tem equação com essa carinha aqui:
E ela intercepta com os eixos coordenados quando e . Tá, como eu sei disso?
Bem, quando eu interceptar o eixo , eu sei que precisa valer zero. E o contrário também é verdadeiro, ou seja, quando interceptamos o eixo , vale zero.
Quando
Quando
Passo 3
Feito isto, podemos concluir que a base e altura do nosso triângulo tem comprimentos e , respectivamente.
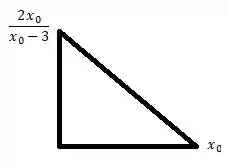
Logo, a área desse triângulo vale quanto?
Passo 4
Queremos encontrar a menor área possível. Toda vez que aparecer as palavrinhas “maior” ou “menor” ou coisas desse tipo, você se lembra o que podemos usar?
Se lembra que quando a gente deriva uma função e iguala ela a zero, encontramos os pontos de máximo ou mínimo dependendo do tipo de problema?
Então é exatamente isso que iremos fazer: vamos derivar nossa função, igualar a zero e depois pegar esse valor e substituir na função.
Vamos precisar aplicar a regra do quociente aqui!
Note que resolver essa equação, nós dá que .
Logo, o triângulo terá o menor valor de área quando , portanto, substituindo na equação da área em função de , temos:
Resposta
32