UFCG – Cálculo Diferencial e Integral I – Listas - Teste 9 – Listas Cálculo 1- UAMat – Lista 2 – Derivadas – Questão 10d
Determine a equação da reta tangente a cada curva no ponto indicado:
d) em
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma equação e nos pede a equação da reta tangente da curva em um ponto indicado (quando ler “reta tangente em um ponto” já pensa na derivada hehe).
Bom... lembra como determina a equação de uma reta? Bora relembrar olhando a figura abaixo:
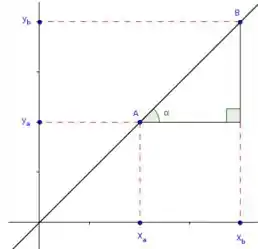
Primeiro, com a posição dos pontos e , a gente encontra a inclinação da reta através da relação .
Depois, aplicamos na equação da reta e descobrimos os valores de e !!
Mas como fazemos isso para um só ponto??? Bom, ao invés de fazer , a gente faz (pois estamos tendendo a zero a distância do ponto ao ponto ) e aplicamos em !!!
Não entendeu? Então bora junto descobrir!! 😉
Passo 2
Seguinte... vamos primeiramente derivar os dois lados da igualdade:
Do lado esquerdo, em e aplicamos a regra da cadeia, em que e seguimos derivando os outros termos normalmente. Assim, temos:
Passo 3
Dessa forma, substituindo o ponto na derivada encontrada, temos:
E, aplicando na equação da reta , temos:
Entendeu direitinho? Responde aee ;)
