UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista de Derivadas 2022.2, Questão 2a
Determine a equação da reta tangente às seguintes curvas, nos pontos indicados. Esboce o gráfico em cada caso:
(a)
Passo 1
Eaew, tudo certinho contigo?
Temos que encontrar a equação da reta tangente à curva
no ponto
Temos que a equação dessa reta tangente é dada por
então o primeiro passo é calcular a derivada de no ponto .
Vem comigo!
Passo 2
Primeiro vamos calcular
então
Passo 3
Temos então que a equação da reta tangente fica
então, a equação da reta tangente é
Passo 4
Nesse caso o esboço do gráfico da curva e da reta tangente no ponto (1,0) é
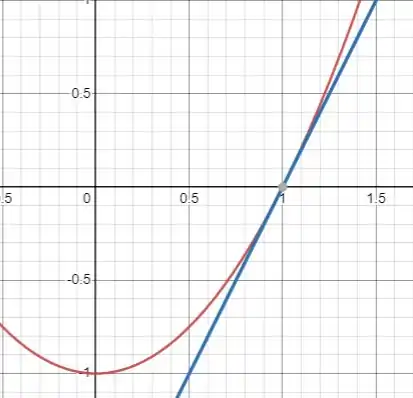
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Exercícios de Livros Relacionados
Encontre f ' ( a ) :f (t) = (2 t + 1)/(t + 3)
Encontre f ' ( a ) .f (x) = sqrt(3 x + 1)
Se um tanque cilíndrico comporta 100000 litros de água, que podem escoar pela base do tanque em uma hora, então a Lei de Torricelli fornece o volume V de água que restou no tanque após t minutos como:
O custo (em dólares) de produzir x unidades de uma certa mercadoria é C x = 5000 +10 x + 0,05 x 2 a) Encontre a taxa média da variação de C em relação a x quando os níveis de produção estiverem varian
Encontre f ' ( a ) . f x = 3 - 2 x + 4 x 2