UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - 1ª Lista - 2022.2, Questão 13
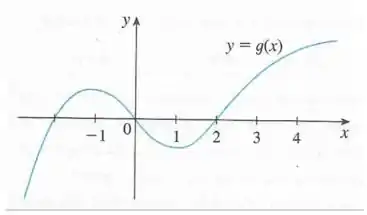
Q13. Escreva na ordem crescente os números , , , e .
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema foi dado um gráfico da função e nosso objetivo é enumerar as derivadas , , , e em ordem crescente...
Tem ideia de como fazemos isso? 🤔
A deriva de uma função nos dá muitas informações... a principal e mais primordial dela é que a derivada de uma função em um ponto resulta na inclinação da reta tangente a esse ponto...
Ou seja, se traçarmos as retas tangentes à função nos pontos indicados, podemos descobrir qual derivada é maior e qual é menor...
Sacou? Bora começar! 😉
Passo 2
Esboçando as curvas tangentes no gráfico de , temos
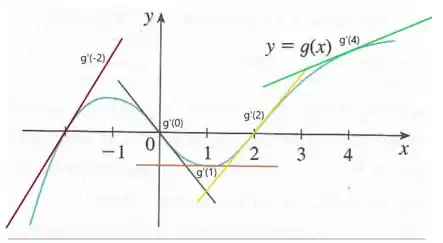
Ordenando as derivadas em ordem crescente de aclividade temos que em a reta tangente é a única que está em “descida” portanto certamente é o menor que e também é o menor valor que temos.
Em vemos que a reta tangente é horizontal, portanto, é igual a , sendo o segundo menor.
Agora, vemos em seguida a inclinação da reta tangente ao ponto é levemente voltada para cima, logo podemos perceber que esse é o terceiro ponto cuja derivada é maior.
Agora em e em vemos que as retas tangentes têm praticamente a mesma inclinação, então podemos dizer que essas derivadas estão empatadas em valor, sendo os dois mais altos...
De forma resumida, temos
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
