Sejam cujos gráficos são:
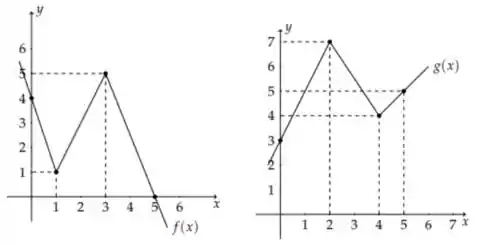
Sejam dadas por e . O valor é:
a) ;
b) ;
c) ;
d) ;
e) .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá dois gráficos de duas funções e e nos diz que e , onde e são funções em .
Queremos descobrir .
Como vamos trabalhar com derivadas, temos que derivar e e depois analisar os gráficos.
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, derivando as funções, temos:
E
Passo 3
Logo, de acordo com os gráficos, temos:
Onde é a inclinação de para e é a inclinação de para .
Assim, continuando, temos:
Passo 4
Para , temos:
Dessa forma:
Entendeu direitinho? Responde aee ;)
