USP – Cálculo I – IME – 2021.1 – Q7
Um triângulo possui dois de seus lados iguais a 3cm e 8cm e o terceiro lado variando com o tempo. Em um certo instante, o lado mede 7cm e está aumentando a uma taxa de . Determine a taxa com a qual o ângulo oposto ao lado está variando neste momento.
Passo 1
E aí, galerinha! Tudo na paz por aí?
Bem, o que a gente consegue extrair de informação desse enunciado, galera?
O primeiro é que temos dois lados de um triângulo com tamanhos fixos e outro que está variando e que queremos saber o ângulo oposto ao lado .
Qual é o ângulo que está sempre ao lado oposto (CATETO OPOSTO)? Nosso lindão cosseno, certo?
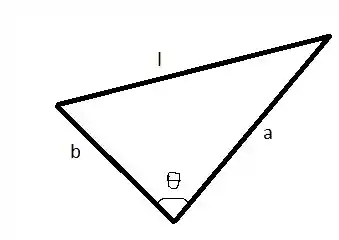
Como conseguimos correlacionar tudo?
Lei dos cossenos!!!
Opa, agora que temos nossa equação que correlacionada tudo, preicamos lembrar o que “taxa de variação” quer dizer. Você se lembra?
Isso tá falando da derivadaaaa!!! Então vamos que vamos aplicar isso!!
Passo 2
Derivando a lei dos cossenos:
Note que quando , (dado do enunciado), podendo encontrar então qual era o ângulo que estava tendo na condição inicial:
Passo 3
Ter um valor de implica dizer que no tempo igual a zero, portanto, podemos ter que na nossa derivação:
A taxa de crescimento de também foi dado no enunciado, logo:
Logo: