UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - UNICAMP (MA111) - Lista 6, Questão 3c
(3) Usando a definição de derivada, prove que
(c) Ilustre os dois casos com o esboço de gráficos.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos que ilustrar graficamente os casos em que se então e se , então .
Tem ideia de como fazer isso? 🤔
Para esboçar esses casos, podemos definir algumas curvas para e e aplicar essas igualdades.
Por exemplo, para o primeiro caso, se , então .
Já no segundo caso se , então .
Sacou? Veja só! 😉
Passo 2
Calculando para o primeiro caso, temos e
Esboçando os gráficos para ...
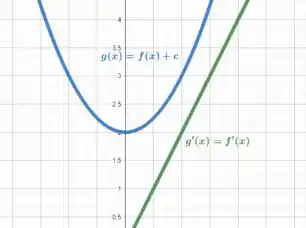
agora para o segundo caso, temos e ...
Esboçando essas curvas no plano cartesiano para , temos
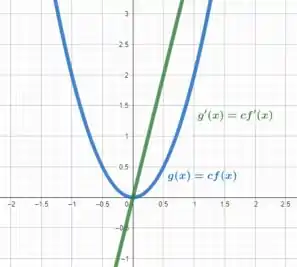
O que achou? Foi de boa? Responde aí! 😊
Resposta
Gráficos no desenvolvimento do problema.
Exercícios de Livros Relacionados
Encontre f ' ( a ) :f (t) = (2 t + 1)/(t + 3)
Encontre f ' ( a ) .f (x) = sqrt(3 x + 1)
Se um tanque cilíndrico comporta 100000 litros de água, que podem escoar pela base do tanque em uma hora, então a Lei de Torricelli fornece o volume V de água que restou no tanque após t minutos como:
O custo (em dólares) de produzir x unidades de uma certa mercadoria é C x = 5000 +10 x + 0,05 x 2 a) Encontre a taxa média da variação de C em relação a x quando os níveis de produção estiverem varian
Encontre f ' ( a ) . f x = 3 - 2 x + 4 x 2