Halliday - Vol. 3 – 9º edição – Capítulo 29 – Seção 3 – Exercício 37
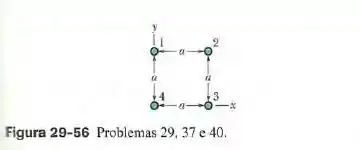
(Capítulo 29.3 – Exercício 37) Na figura 29-56, quatro fios retilíneos são perpendiculares ao papel e suas seções retas formam um quadrado de aldo . Todos os fios conduzem correntes de e as correntes são para fora do papel nos fios 1 e 4 e para dentro do papel nos fios 2 e 3. Em termos dos vetores unitários, qual é a força magnética por metro de fio que age sobre o fio 4?
Passo 1
Faaaala pessoal, vamos lá pra mais uma!
Nesse exercício, temos 4 fios conduzindo correntes, e queremos encontrar qual a força magnética por metro de fio que age no fio 4
A força entre duas correntes paralelas na presença do campo magnético externo é dada por:
em que é o vetor comprimento do fio. Os vetores e são mutuamente perpendiculares e, portanto, de acordo com a equação para fios retilíneos longos, podemos escrever:
As forças no fio 4 podem ser decompostas da seguinte forma:
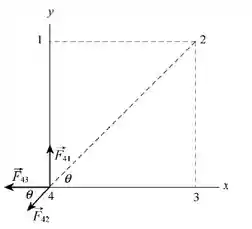
Como estamos lidando com uma disposição dos fios no formato de um quadrado, uma maneira de calcularmos a força magnética no fio 4 pode ser através da decomposição dos vetores de força em componentes e . A figura a seguir mostra essa situação.
Passo 2
Como porque estamos falando de um quadrado, podemos escrever as seguintes relações:
Tendo isso em mãos, podemos calcular o valor de ! Sabemos do teorema de pitágoras que:
O ângulo que faz com o semieixo positivo é:
Passo 3
Na notação dos vetores unitários, temos:
Arrasamos!
Resposta
A força magnética por metro de fio é::