2 - Sabemos que um capacitor de placas paralelas (com o diâmetro das placas muito maior que a distância entre elas) possui a propriedade de confinar o campo elétrico em seu interior. Essa propriedade se generaliza para capacitores das mais variadas formas. Da mesma maneira, podemos pensar em sistemas magnéticos análogos ao capacitor (sistemas que possuem campo magnético confinado ao interior de uma determinada região). Pensando nisso, considere os quatro sistemas abaixo:
I - Solenoide infinito (comprimento do solenoide muito maior que seu raio) com corrente .
II - Solenoide finito (comprimento do solenoide da mesma ordem de grandeza que seu raio) com corrente I.
III - Cabo coaxial com correntes I e -I (sentidos opostos).
IV - Cabo coaxial com correntes I e I (mesmo sentido).
- Apenas I e III representam sistemas que confinam campo magnético em seus interiores.
- Os sistemas I e III confinam o campo magnético em seus interiores, enquanto nos sistemas II e IV o campo magnético confinado é nulo.
- Todos os sistemas (I, II, III e IV) confinam o campo magnético em seus interiores.
- Os sistemas II e IV confinam o campo magnético em seus interiores, enquanto nos sistemas I e III o campo magnético confinado é nulo.
- Apenas II e IV representam sistemas que confinam campo magnético em seus interiores.
Passo 1
Ora bolas, sabemos que confinar um campo (no caso magnético) é deixa-lo preso de forma que não se tenha campo fora dele!
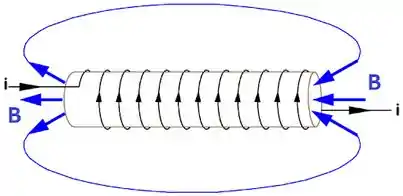
Um solenoide infinito é desse tipo aqui:

Repare que a corrente pela regra da mão direita gera um campo dentro do solenoide, mas do lado de fora, o campo é . Isso acontece por que quando a corrente passa de um lado, ela até gera um campo do lado de fora, mas quando ela passa do lado oposto, ela gera um campo apontado no sentido oposto! Cancelando o campo do lado de fora, saca?
Então de fato aqui o campo fica confinado!
Passo 2
Já quanto a um solenoide finito...
Não acontece o confinamento como no solenoide infinito! O motivo é justamente porque ela é finita e então o campo deve formar uma linha fechada: passando por dentro, saindo e voltando pelo outro lado!
Passo 3
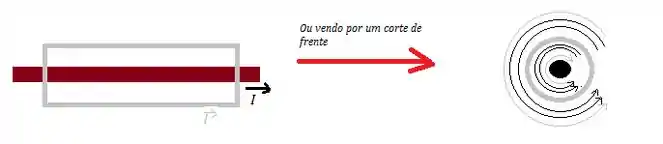
Um cabo coaxial é desse tipo aqui:

Se passarmos uma corrente interna (indo para a direita ou saindo da tela) e passarmos outra no sentido oposto ()...
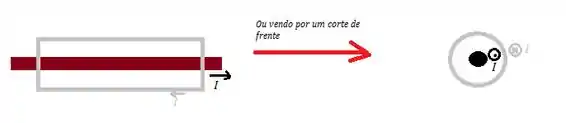
De acordo com a regra da mão direita, o sentido do campo magnético feito ela corrente que sai no interior do cabo será:
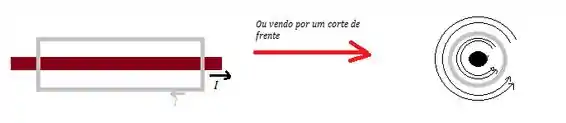
Já o campo magnético pela corrente que entra pela casca cinza, no interior e no exterior, ela terá sentidos diferentes:
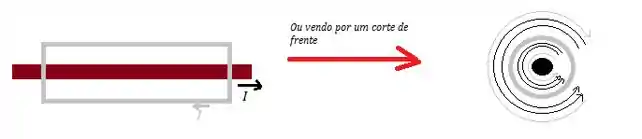
Veja que do lado de fora, os campos se cancelam, tornando o campo total nulo! Já do lado de dentro, os campos se somam, ficando confinados no interior!
Passo 4
Para corrente de mesmo sentido no cabo coaxial o efeito será o contrário: elas vão se cancelar no interior, mas vão se somar do lado de fora?
Logo, o campo não estará mais confinado!
Passo 5
Perceba então, que o campo magnético só ficará preso dentro do solenoide infinito, ou dentro do cabo coaxial de correntes opostas!
Resposta
Letra A.