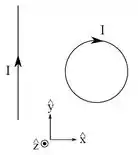
Considere um sistema formado por um fio fino, retilíneo e infinito coplanar a uma espira circular, como mostrado na figura abaixo. Tanto o fio retilíneo quando a espira circular transportam correntes estacionárias de intensidade , com os sentidos indicados na figura. Nessa situação, podemos afirmar que o sentido das forças que o fio exerce sobre a espira, e que a espira exerce sobre o fio são, respectivamente:

7. Não haverá força resultante sobre o fio e a espira.

Como a espira é simétrica, os vetores atuando sobre os comprimentos à esquerda e à direita de uma linha vertical que divide a espira ao meio, possuem componentes ao longo da direção  e .

À esquerda da linha tracejada, as componentes de ao longo de  se cancelam aos pares, enquanto as componentes ao longo de  se somam.

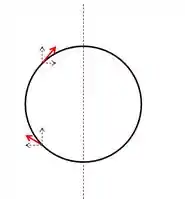
Com isso, no lado esquerdo teremos algo desse tipo:

E isso resulta em uma força que aponta para .

Vamos analisar agora o lado direito:

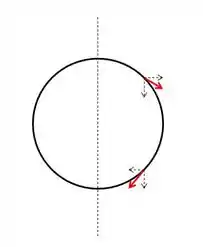
As componentes de ao longo de  se cancelam aos pares, enquanto as componentes ao longo de  se somam.

Com isso, no lado esquerdo teremos algo desse tipo:

Resultando em uma força que aponta para .

Para fechar, como o campo magnético devido ao fio retilíneo é mais intenso na extremidade esquerda da espira, já que o fio está mais próximo dessa parte, então a força resultante   é mais intensa que a força resultante   .

Por isso, a força resultante total sobre a espira estará ao longo da direção . Por outro lado, a força que atua sobre o fio está na mesma direção, mas em sentido contrário, ou seja, sobre o fio a está ao longo de , pela terceira lei de Newton.