Considere os dois fios condutores mostrados na figura abaixo. Um deles é retilíneo e infinito, enquanto o outro é retilíneo e infinito, exceto por uma parte dobrada na forma de um semicírculo de raio .
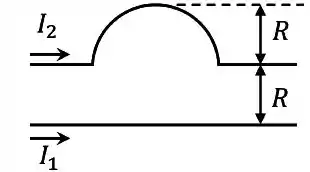
Os fios carregam correntes estacionárias de intensidades e no mesmo sentido, respectivamente, e a distância entre eles também vale . Qual deve ser a razão para que o campo magnético no centro do semicírculo seja nulo?
;
;
;
;
;
O campo nunca pode ser nulo neste ponto, pois as correntes tem o mesmo sentido.
Passo 1
O campo magnético no centro do circulo será igual à soma vetorial dos campos gerados pelos dois fios. Uma vez que o campo gerado pelo fio com corrente atua na direção saindo do plano e o campo gerado pelo fio com corrente atua na direção entrando no plano, para que o mesmo seja nulo, é necessário que:
Passo 2
O módulo do campo magnético gerado por um fio infinito é dado por:
Neste caso, o fio infinito conduz a corrente e está a uma distância do centro da circunferência, logo:
Passo 3
O campo magnético gerado pela semicircunferência é determinado pela Lei de Biot-Savart, dada por:
Como estamos interessados no módulo campo gerado pela semicircunferência que conduz corrente , teremos:
Neste caso, é constante e vale . O infinitesimal correspondente a um pedaço infinitesimal do fio, como se trata de uma semicircunferência, será:
Logo:
Passo 4
Finalmente:
Simplificando o que dá para simplificar, teremos:
Finalmente:
A resposta é a letra .
Resposta
;