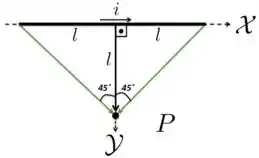
O arranjo ilustrado na figura abaixo é composto por seis fios retilíneos finitos de comprimento . A corrente elétrica que circula em tal arranjo é . Usando a lei de Biot-Savart, calcule:
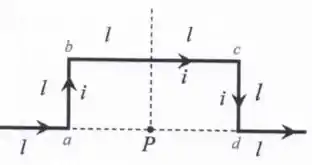
- O módulo do campo magnético no ponto devido ao fio localizado ao longo do segmento .
- O módulo do campo magnético no ponto devido aos fios localizados ao longo do segmento .
- O módulo, direção e sentido do campo magnético total no ponto .
Passo 1
É fundamental que nos lembremos aqui do seguinte: uma corrente que passa em um elemento de um condutor produz um campo magnético em um ponto a uma distância de . Esse vetor campo magnético tem expressão dada pela lei de Biot-Savart
sendo o vetor unitário que aponta de para o ponto onde queremos calcular o campo . Para fixar o que é cada termo da expressão acima, vamos dar uma olhada para a figura abaixo, em que colocamos o ponto sobre o eixo a uma distância da origem e vetor é orientado sempre na direção e sentido da corrente que passa no condutor.
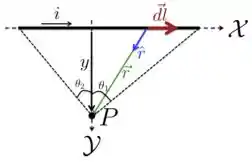
O campo magnético vai ter direção e sentido dado pelo produto vetorial , em que é o ângulo entre e e o produto vai estar entrando no plano da página e será perpendicular a ela.
Agora, colocando cada termo de acordo com a figura, temos que e (módulo de um vetor unitário é!). Outra coisa que já podemos fazer é desconsiderar as duas partes do fio que estão na horizontal, pois eles não contribuem para o campo no ponto , uma vez que e e para esses casos.
Passo 2
Vamos continuar nossa solução focando na próxima figura abaixo.
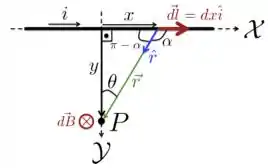
Olhando para esse desenho, podemos escrever que o módulo do campo magnético é
Agora, vamos calcular no ponto levando em conta, primeiro, o ângulo da figura acima e depois integrando esse ângulo entre e da figura do Passo 1. Do triângulo retângulo da figura acima, vemos que
Além disso, temos também
Derivando essa expressão em relação , obtemos
Juntando tudo isso:
Como , podemos simplicar a expressão acima.
E agora basta integrar de a (dá um olhada na figura do Passo 1 para entender porque integraremos assim!):
Essa expressão é interessante, porque pode te ajudar em outros problemas mais gerais do que este…
Uma vez que temos essa expressão geral, agora podemos aplicar para o caso particular do nosso problema, aplicando para cada pedaço do condutor.
Passo 3
a) Para o lado da figura do enunciado, basta aplicarmos na expressão acima: , e , como podemos ver na figura abaixo.
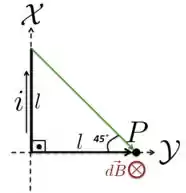
Campos produzidos pela corrente nos trechos e :
Os campos de e de têm o mesmo módulo igual a
Ambos os campos estão entrando no plano da página e são perpendiculares a ela, ou seja, estão na direção e sentido de .
Passo 4
b) Campos produzidos pela corrente no trecho :
De acordo com a figura abaixo, neste caso temos e .
Por isso, o módulo do campo devido a esse trecho será
e tem a direção e o sentido de .
Passo 5
c) Todos os campos que acabamos de calcular terão direção e sentido perpendiculares à página e entrando nela. Por isso, o campo magnético total no ponto será: