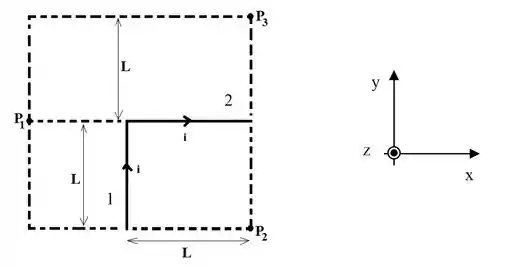
A figura mostra dois fios condutores de corrente. A corrente no fio tem o sentido positivo do eixo e a corrente no fio tem o sentido positivo do eixo . Com esta escolha de sistemas de coordenadas, o sentido positivo do eixo é para fora do papel. As corrente nos fios e são iguais a .
Utilizando explicitamente a lei de Biot-Savart:
Calcule o campo magnético gerado no ponto pela corrente no fio .
Calcule o campo magnético gerado no ponto pela corrente no fio
Calcule o campo magnético total gerado no ponto pelas correntes dos fios e .
Passo 1
Para determinar o campo magnético, vamos, assim como pede o enunciado, utilizar a lei de Biot-Savart, ela nos diz:
Podemos ver pela figura que o produto vetorial dá zero, pois os vetores são antiparalelos, temos portanto:
Lembre-se que é o vetor que vai do fio, até o ponto em que queremos saber o campo, e é o vetor unitário da direção da corrente(fio).
Passo 2
Aplicando a Lei de Biot-Savart, temos:
Para nossa configuração, temos:
Pela regra da mão direita, temos que o campo aponta na direção , o campo fica assim:
Onde é o angulo entre os vetores e , da figura, podemos tirar as seguintes conclusões:
Substituindo na equação, temos:
Resolvendo essa integral, temos:
O campo produzido em é:
Calma, essa integral não foi tirada da cartola, ela está na capa da prova. Sempre que cair uma integral difícil, olha a capa da prova e procura ela lá!
Passo 3
Para determinar o campo total no ponto , vamos calcular o campo gerado por cada fio separadamente, começando pelo fio . Vamos usar o mesmo mimimi que usamos no itemanterior. Pela Lei de Biot-Savart, temos:
Para nossa configuração, temos:
Pela regra da mão direita, temos que o campo aponta na direção , o campo fica assim:
Onde é o angulo entre os vetores e , da figura, podemos tirar as seguintes conclusões:
Substituindo na equação, temos:
Resolvendo essa integral, temos:
A contribuição do fio , será:
Vamos ao fio !
Passo 4
Para achar a contribuição do fio vamos fazer exatamente o que fizemos no item . Se liga!
Aplicando a Lei de Biot-Savart, temos:
Para nossa configuração, temos:
Pela regra da mão direita, temos que o campo aponta na direção , o campo fica assim:
Onde é o angulo entre os vetores e , da figura, podemos tirar as seguintes conclusões:
Substituindo na equação, temos:
Resolvendo essa integral, temos:
A contribuição do fio , será:
A soma das contribuições nos dá o campo total no ponto
Resposta