. Considere a espira condutora mostrada na figura abaixo. Ela é formada pela junção de dois trechos semicirculares de raios e com dois trechos retilíneos e conduz uma corrente estacionária de intensidade no sentido indicado.
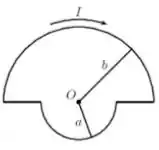
Deduza, em detalhe, uma expressão para o vetor campo magnético produzido pela espira
no ponto , que corresponde ao centro comum dos trechos semicirculares.
Passo 1
Vem comigo que a gente vai detonar esse problema.
Ele quer que encontremos uma expressão para o campo magnético da espira no ponto .
Podemos usar o princípio da superposição e dizer que o campo resultante é dado pela soma do campo produzido por uma semicircunferência da espira com o campo da outra, assim:
Como essas duas partes são semicircunferências só mudando o raio a forma de encontrar o campo é a mesma, então podemos encontrar o campo para uma delas e o da outra vai ser exatamente igual, só mudando o raio.
Para encontrar esse campo então vamos usar a lei de Biot-Savart, dada por:
Onde é o comprimento infinitesimal da espira e esse vetor é tangente a espira e é o vetor unitário que dá a direção esse comprimento ao ponto .
Agora temos que ver como se comporta o produto vetorial em cada parte da espira.
Passo 2
Vamos fazer essa analise então e para isso vamos considerar a parte de raio da espira.
Nas duas partes horizontais onde temos e na mesma direção temos que esse produto vetorial vai ser zero, logo essas partes não contribuem para o campo.
Agora nas partes semicirculares temos que é perpendicular logo esse produto vetorial nos dá:
O sinal negativo indica que esse novo vetor aponta na direção negativa de e lembrando que é um vetor unitário, temos:
Jogando isso na lei de Biot-Savart para a espira de raio , temos:
Agora para achar o campo temos que integrar essa expressão.
Passo 3
Vamos a essa integração então, temos:
Essa integral em representa o comprimento de toda a espira de raio e o comprimento de um semicírculo é , assim:
Como eu falei no passo esse é o mesmo processo para o cálculo do campo da espira de raio , só mudando o raio, assim:
Passo 4
Com isso que encontramos temos que o campo total em vai ser dado por:
Então temos que:
Esse é o campo produzido pela espira no ponto .