Um fio retilíneo de comprimento é percorrido por uma corrente como mostrado na figura ao lado (o sentido da corrente está indicado no desenho). O fio repousa sobre o eixo e suas extremidades estão nas coordenadas .
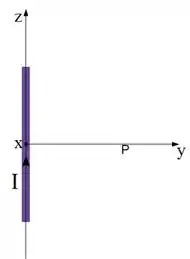
A partir da lei de Biot-Savart, encontre o vetor campo magnético no ponto mostrado na figura cuja coordenada é . (Considere
Partindo do resultado do item anterior, encontre o campo magnético para um fio muito longo .
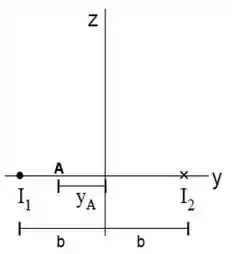
Considere agora dois fios retilíneos muitos longos paralelos percorridos por correntes saindo e entrando no papel, respectivamente.
A partir do campo magnético encontrado no item , encontre o campo magnético resultante no ponto mostrado na figura.
Passo 1
Para determinar o campo magnético no ponto , gerado pelo fio, vamos começar calculando o campo gerado por um pedaço infinitesimal do fio, vamos começar relembrando da Lei de Biot-Savart:
Vamos pegar um comprimento infinitesimal do fio!
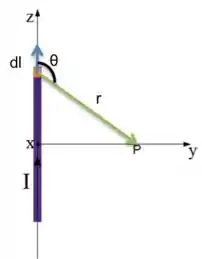
Analisando a figura, temos , o comprimento infinitesimal do fio, , o vetor que aponta na direção do ponto e o ângulo entre os vetores e . Agora sim, podemos dar uma melhorada na Lei de Biot-Savart, nos livrando do produto vetorial, repare que aponta na direção , temos então:
Para determinar , devemos pensar, que para cada valor de , temos que será a hipotenusa de um triângulo retângulo cujos catetos são e , ou seja, para , temos:
beleza, agora falta só determinar , nós já sabemos que o , e no nosso caso, é mais simples trabalhar com pois esse é o ângulo entre e , ou seja:
Beleza, agora é só substituir e calcular o campo, simbora!!
Como queremos integrar ao longo de todo fio, temos:
O mais lindo de tudo é que essa integral feiosa é dada na capa da prova(Uhuuulll)!
Passo 2
Para um fio muito longo, ele nos diz que , isso quer dizer que . Colocando em evidência dentro da raiz do resultado do campo que obtivemos no item , temos:
Repare que temos dentro da raiz a razão , como ela é muito menor que , temos:
Ou seja, para um fio longo, temos:
Passo 3
Agora que temos o resultado do item , fica fácil de resolver esse item! Pela figura, temos que o fio está a uma distância do ponto . Além disso, usando a regra da mão direita, temos que no ponto o campo aponta no sentido positivo do eixo , ou seja, a corrente no ponto devido à este fio é:
Para o segundo fio, temos que a distância até o ponto é , além disso, usando a regra da mão direita, temos que no ponto o campo aponta no sentido positivo do eixo , ou seja, a corrente no ponto devido à este fio é:
Somando os dois campos, temos:
Resposta