Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Biot-Savart Geral

Ver Teoria
Exercício 151234567891011121314161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778

Enunciado

Lei de Biot-Savart

Dois fios muito longos são percorridos por correntes elétricas estacionárias de mesma intensidade. Cada um de tais fios é constituído por dois segmentos retilíneos (muito longos) e por um arco circular intermediário (com abertura de 90 º ); os raios de tais arcos são tai que R I I > R V . Qual dos segmentos dá maior contribuição para o campo magnético resultante B → C no ponto central C ?

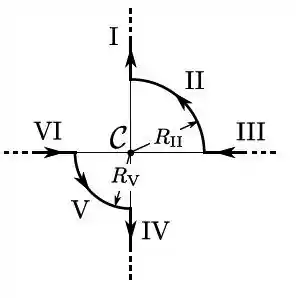
  1. II
  2. V
  3. I e III
  4. IV e VI
  5. Todos contribuem igualmente para B → ( C ) .

Passo 1

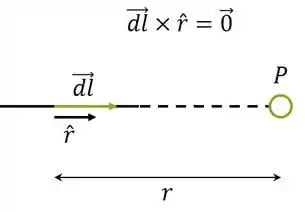
Pela lei de Biot-Savart:

B → = μ 0 4 π ∫ f i o I d l → × r ^ r 2

Primeiramente fazemos os produtos vetoriais dos fios retilíneos e mostramos que eles fazem campo nulo:

Passo 2

Agora vamos fazer os segmentos circulares. Sabemos que em cada um deles temos r = R constante e a corrente também:

B → = μ 0 I 4 π R 2 ∫ f i o d l → × r ^

Seja z ^ o sentido saindo da tela. Fazendo o produto vetorial para um segmento semicircular genérico:

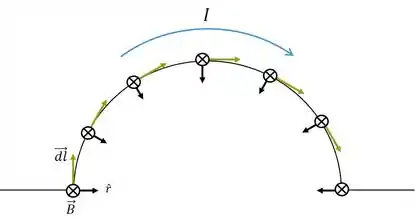
Temos:

B → = μ 0 I 4 π R 2 z ^ ∫ f i o d l

O comprimento é um quarto de circunferência:

B → = μ 0 I 4 π R 2 z ^ 2 π R 4

B → = μ 0 I 8 R z ^

Passo 3

Portanto para cada um dos segmentos temos:

B → V = μ 0 I 8 R V z ^

B → I I = μ 0 I 8 R I I z ^

Agora queremos saber quem dá mais. Como: R I I > R V

Segue:

1 R I I < 1 R V

Passo 4

Multiplicando ambos os lados por μ 0 I / 8 :

μ 0 I 8 R I I < μ 0 I 8 R V

B I I < B V

Ou seja, o segmento V é quem dá mais.

Resposta

Letra b

Exercícios de Livros Relacionados

14- Uma partícula com carga 6.40 × 10 - 19C se desloca ao longo de uma órbita circular com raio igual a 4.68m m , em virtude da força oriunda de um campo magnético de módulo 1.65T , cuja direção é per
15- Um elétron no ponto A da Figura 27.46 possui velocidade v 0 igual a 1.41 × 10 6m / s . Determine: ( a ) o módulo, a direção e o sentido do campo magnético que obriga o elétron a descrever uma órbi
16- Repita o Exercício 27.15 para o caso no qual a partícula é um próton em vez de um elétron.
Dois fios longos estão no plano x y e conduzem correntes no sentido positivo do eixo x . O fio 1 está em y = 10,0c m e conduz uma corrente de 6,00A ; o fio 2 está em y = 5,00c m e conduz uma corrente
Na figura 29-63, cinco fios paralelos longos no plano x y estão separados por uma distância d = 8,00c m , têm 10,0m de comprimento e conduzem correntes iguais de 3,00A para fora do papel. Em termos do