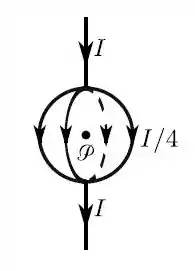
Uma corrente estacionária, de intensidade , flui ao longo de um segmento retilíneo que se divide, igualmente, em quatro meridianos de uma esfera de raio , perpendiculares (dois a dois) entre si, e reencontrando-se num outro segmento retilíneo. Qual é o módulo do campo magnético no centro da esfera?
Passo 1
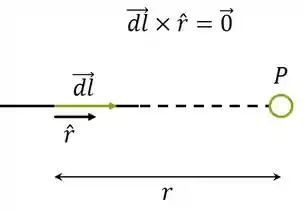
Achar campo magnético de fios circulares ou semicirculares é pato pra Lei de Biot-Savart. Enunciando:
Podemos mostrar que o campo dos segmentos retilíneos no ponto é zero:
Passo 2
Logo, nos resta calcular as quatro integrais dos segmentos circulares. O truque neste caso seria se aproveitar da simetria. Podemos calcular o campo para um par de segmentos e reproduzir o resultado rapidamente para os outros.
No caso, se rodarmos a Lei para um par simétrico de segmentos semicirculares, podemos ver que eles se anulam:
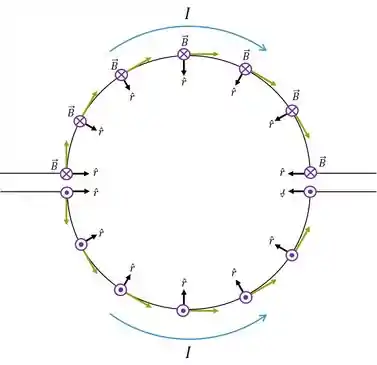
Portanto o campo desse par vai ser zero no ponto . Analogamente, o outro par vai zerar também. O campo total é:
Resposta
Letra c