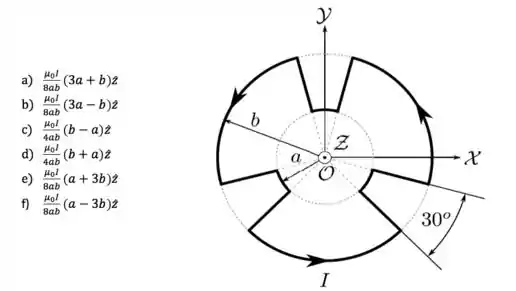
Uma corrente estacionária de intensidade percorre um circuito condutor que se encontra no plano de um sistema de coordenadas, como mostrado na figura abaixo. Esse circuito é formado por 3 arcos de circunferência idênticos de raio e ângulo central de , por outros 3 arcos de circunferência idênticos, de raio () e por segmentos de reta radiais que conectam os arcos, como indicado. Nessa situação, o campo magnético gerado por esse circuito no ponto vale:
Passo 1
Na primeira olhada que a gente dá nessa questão, de cara essa figura já assusta, ou não? Kkk Bom, espero te convencer de que esse problema não tem essa “cara toooda de maldade”! Bora lá?
Bom, a primeira coisa que a gente precisa verificar é o sentido do campo magnético produzido pela corrente que circula no sentido anti-horário. Pela regra da mão direita, vemos que o sentido e direção do campo magnético é dado por .
Conferiu e concorda com isso? Checa isso para treinar como determinar o sentido e direção do campo magnético produzido por uma corrente estacionária, pois isso é bastante importante nessa parte do conteúdo.
“Saber qual sentido do campo nessa questão não ajuda em nada, querido professor, porque todas as respostas estão na direção ” rsrs.
Mas já dá para eliminar, com certeza, o item f), porque, como (enunciado), e nos leva a reescrever o item f) como:
que está na direção e sentido de e sabemos que isso não pode acontecer, pois vimos e concordamos (espero!) que o campo deve estar na direção e sentido de pela regra da mão direita!!
Já eliminamos UM ITEM \0/ Agora são só outros 5....
Passo 2
A equação que nos dá como é o campo magnético produzido por uma corrente estacionária é dada pela lei de Biot-Savart, que tem a seguinte forma diferencial:
sendo é o vetor que dá o elemento de comprimento pelo qual passa a corrente e o vetor está relacionado à distância do elemento ao ponto onde a corrente produz o campo.
Primeira coisa importante nessa expressão: o produto vetorial !! Esse produto dá sempre um vetor que é perpendicular ao elemento e também ao vetor unitário . Portanto, o campo produzido pela corrente é sempre perpendicular tanto ao percurso, e portanto perpendicular à corrente, quando à distância .
Segundo aspecto importante: uma corrente paralela ao vetor não produz campo na direção . Ou seja, todos elementos do Tipo (destacado em azul na figura) não contribuem para o campo magnético em , pois os respetivos elementos são paralelos aos vetores , como mostram os vetores correspondentes na figura.
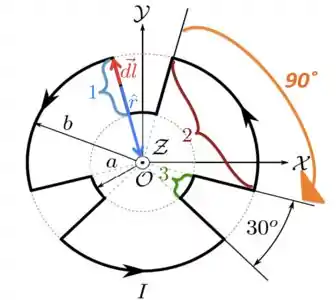
Portanto, podemos esquecer os elementos do Tipo da figura e focar agora naqueles dos Tipos 2 e 3, porque são apenas esses elementos que contribuem para o campo no centro .
Passo 3
Na figura, temos 6 arcos de círculo, sendo que aqueles do Tipo compreendem um arco de e aqueles do Tipo compreendem um arco de . Por isso, temos o seguinte: .
Para uma corrente estacionária percorrendo um arco de círculo que compreende um ângulo (em radianos!) qualquer, o campo magnético gerado em um posição arbitrária é dado por:
Essa é uma expressão importante para se ter em mente. Por exemplo, se , temos o campo gerado por uma espira circular de raio em seu centro!!
Agora ficou fácil, porque na figura acima, temos 3 arcos de círculo com , com , e outros 3 arcos com , com raio . Colocando essas informações dentro da expressão acima para o campo, temos
Resposta
Portanto, a resposta correta é a letra a) .