Considere uma espira quadrada de lado percorrida por uma corrente . A espira se encontra no plano , conforme a figura.
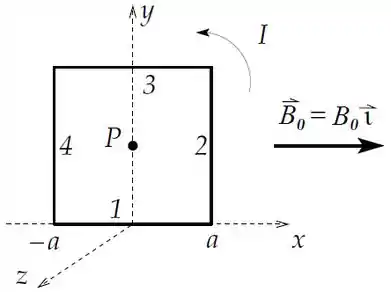
Determine o campo magnético produzido pela espira no seu centro .
Sugestão: Calcule o campo produzido pelo lado e use a simetria do problema.
Passo 1
Determine o campo magnético produzido pela espira no seu centro .
Vamos usar a sugestão do problema e calcular o campo magnético apenas do fio 1.
Nesse caso, vamos ter que recorrer à Lei de Biot-Savart:
Como a corrente é constante, podemos simplificar a equação para:
Pra começar, vamos dar uma olhada nos vetores e . Lembrando que está sempre na direção e sentido da corrente.
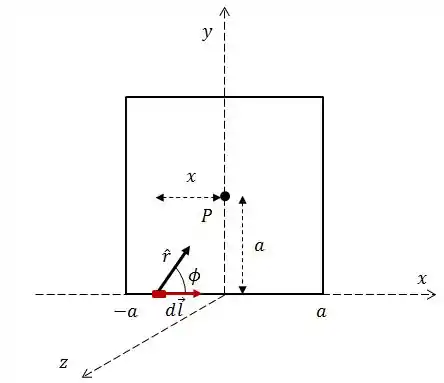
Na figura acima podemos ver que . Além disso:
Agora sim, podemos voltar para a Lei de Biot-Savart:
Onde:
Logo:
Caiu nessa integralzinha marota?! Ela costuma aparecer bastante nesse tipo de questão em que o problema te pede pra calcular o campo magnético de um fio finito.
Relaxa, obviamente ela tem uma solução, e se ela aparecer na sua prova, a solução dela provavelmente estará no seu formulário. Vou facilitar a nossa vida aqui e colocar logo a solução dela:
Substituindo os valores:
Pela simetria do problema, o campo magnético gerado pelos 4 fios retilíneos serão iguais, logo:
Resposta