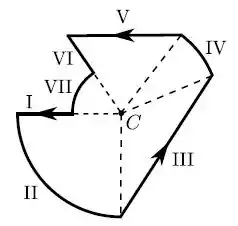
Considere o circuito da figura abaixo, constituído por segmentos retilíneos (I, III, V e VI) e segmentos de arco de círculos (II, IV e VII) concêntricos com o ponto , percorridos por uma corrente estacionária , com sentido assinalado. Indique quais de tais segmentos dão uma contribuição não nula para o campo magnético resultante no ponto .
- II, III, IV, V e VII
- I, III, V e VI
- II, IV e VII
- I, II, IV, VI e VII
- Todos criam campo magnético não nulo em
Passo 1
O campo magnético de uma distribuição continua de corrente é dado pela Lei de Biot-Savart:
Para sabermos quais segmentos dão uma contribuição não nula para o campo magnético resultante do ponto C precisamos analisar o produto vetorial para cada segmento.
Passo 2
Para o segmento I os vetores e são antiparalelos, ou seja, formam um ângulo de e nesse caso:
Para o segmento VI os vetores e são paralelos, ou seja, formam um ângulo de 0° e nesse caso:
De maneira geral, podemos mostrar que segmentos retilíneos que estão alinhados na direção não contribuem para o campo, pois:
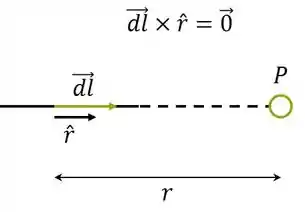
Desse modo, temos que os segmentos I e VI possuem contribuições NULAS para o campo no ponto C, assim já eliminamos as alternativas b, d, e.
Passo 3
Para os demais segmentos (II, III, IV, V e VII) os vetores e não estão alinhados de modo que:
Assim, o campo produzido por esses segmentos no ponto C é não nulo. Desse modo, eliminamos a letra c e já temos nossa resposta. =)
Resposta
Letra a