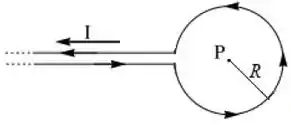
Considere o sistema na figura abaixo, formado por um fio infinito que, em um certo ponto, é enrolado formando uma espira circular de raio . Calcule o campo magnético no centro da espira.
(a)
(b)
(c)
(d)
(e)
Passo 1
Aqui, vamos utilizar a lei de Biot e Savart para calcular o campo no centro da espira.
Temos:
onde é a distância do elemento até onde o campo é medido.
Vamos olhar, inicialmente, para a contribuição da parte reta do fio:
- Como e estão alinhados, ;
- Portanto, .
Passo 2
Já na parte curva do fio, e são ortogonais entre si, como na figura abaixo.
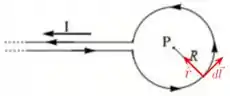
Temos, então:
Resposta
(e)
Exercícios de Livros Relacionados
14- Uma partícula com carga 6.40 × 10 - 19C se desloca ao longo de uma órbita circular com raio igual a 4.68m m , em virtude da força oriunda de um campo magnético de módulo 1.65T , cuja direção é per
15- Um elétron no ponto A da Figura 27.46 possui velocidade v 0 igual a 1.41 × 10 6m / s . Determine: ( a ) o módulo, a direção e o sentido do campo magnético que obriga o elétron a descrever uma órbi
16- Repita o Exercício 27.15 para o caso no qual a partícula é um próton em vez de um elétron.
Dois fios longos estão no plano x y e conduzem correntes no sentido positivo do eixo x . O fio 1 está em y = 10,0c m e conduz uma corrente de 6,00A ; o fio 2 está em y = 5,00c m e conduz uma corrente
Na figura 29-63, cinco fios paralelos longos no plano x y estão separados por uma distância d = 8,00c m , têm 10,0m de comprimento e conduzem correntes iguais de 3,00A para fora do papel. Em termos do