11 - O circuito ao lado transporta uma corrente . Considere as seguintes afirmações:
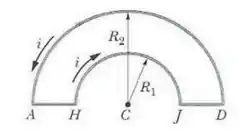
(I) As porções AH e JD não contribuem para o campo magnético produzido no ponto C.
(II) As porções semicirculares HJ e DA não contribuem para o campo magnético produzido no ponto C.
(III) A maior contribuição para o campo magnético produzido no ponto C vem da porção semicircular DA.
(IV) A maior contribuição para o campo magnético produzido no ponto C vem da porção semicircular HJ.
Destas quatro afirmações, as corretas são:
- (I) e (III).
- Todas.
- Nenhuma.
- (I) e (IV).
- (I), (II) e (IV).
Passo 1
Ora! Vamos verificar item a item e ver o qual a alternativa correta! Bora?
- As porções AH e JD não contribuem para o campo magnético produzido no ponto C.
Ora, sabemos que o campo magnético produzido por um trechinho de cargas em movimento pode ser dado por:
Onde é a distância até o ponto que estamos interessados e é o vetor de direção da corrente até o ponto onde estamos medindo. Veja:
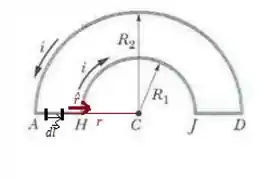
O basicamente é o caminho da corrente, e o é a direção de um trechinho curto da corrente como eu desenhei pra você!
Bem, como no trecho AH, a corrente tem basicamente a direção paralela ao , o produto vetorial deles é , afinal, vetores paralelos possuem produto vetorial nulo. Uma forma de ver isso é sabendo da definição de produto vetorial:
Onde é o ângulo entre os vetores (como são vetores paralelos, ):
Saca? Então...
O que significa que em todo trecho AH e também no JD onde é paralelo ao , não há contribuições do campo magnético!
Então (i) é verdadeiro.
Passo 2
(II) As porções semicirculares HJ e DA não contribuem para o campo magnético produzido no ponto C.
Ora, para não contribuir, tem que ser paralelo como vimos. Nesse caso, eles não serão paralelos e sim perpendiculares!
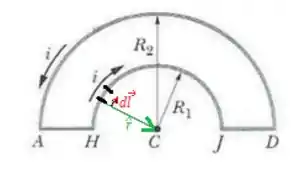
Veja que o em vermelho (direção do pedacinho de corrente) é de fato perpendicular ao . Isso significa que haverá sim, contribuições de todo o trecho HJ assim como o de DA.
Item (ii) é falso.
Passo 3
Vamos analisar agora as duas últimas que estão correlacionadas:
(III) A maior contribuição para o campo magnético produzido no ponto C vem da porção semicircular DA.
(IV) A maior contribuição para o campo magnético produzido no ponto C vem da porção semicircular HJ.
Se uma for mentira, a outra será verdade, já que vimos no passo anterior que as duas influenciam o campo magnético no ponto C.
Então quem contribui mais? Se observarmos a equação que nos dá o campo magnético de acordo com o trechinho de corrente...
Veja que ele está relacionado com distância (inversamente dependente). Ou seja, quanto menor , maior será. Qual trecho tem o menor raio?
ISSO! HJ! Então ele é o trecho de maior influencia!
Item (III) é falso e o item (IV) verdadeiro!
Resposta
Letra D.