Uma espira condutora circular de raio é posicionada sobre o plano de um sistema de coordenadas com seu centro sobre a origem, como mostrado no lado esquerdo da figura abaixo. Ela transporta uma corrente estacionária de intensidade , no sentido indicado.
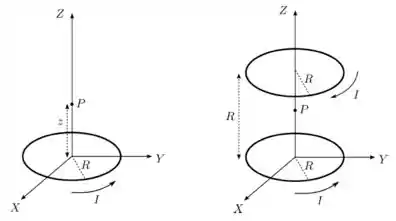
- Utilizando a lei de Biot-Savart, determine o campo magnético produzido pela espira (módulo, direção e sentido) em um ponto localizado sobre o eixo .
- Uma segunda espira, idêntica à primeira, é posicionada paralelamente ao plano com centro no ponto . Ela transporta uma corrente estacionária de mesma intensidade , mas em sentido oposto ao da primeira, como indicado no lado direito da figura. Determine o campo magnético total (módulo, direção e sentido) produzido pelas duas espiras no mesmo ponto .
- Determine o campo magnético total quando .
Passo 1
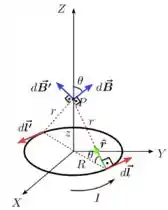
O veto do campo magnético que ela produz é dado por
em que é um vetor que é sempre tangente à curva e tem a mesma direção e sentido da corrente, é o vetor unitário que sempre aponta de para o ponto onde queremos calcular e á distância da espira até esse ponto.
Outra coisa muito importante aqui é direção e sentido do campo magnético, que é dado pelo produto vetorial , o que significa que é sempre perpendicular tanto a quanto à , ou seja, é perpendicular ao plano formado por estes dois vetores.
O módulo desse produto vetorial é
sendo que é o ângulo entre esses dois vetores e usamos que .
Passo 2
a) Passando isso que revisamos para o caso do nosso problema, os elementos e , que estão na figura acima, produzem campos de mesma intensidade, já que estão à mesma distância de , mas as direções e sentidos deles são diferentes.
Tanto quanto fazem um ângulo com o eixo . Portanto, para encontrarmos o campo magnético resultante , basta fazermos:
em que
e
uma vez que é perpendicular ao vetor (), que faz com que .
Agora, precisamos integrar isso:
Nessa integral, o denominador é um número constante, por isso podemos tirá-lo da integral, o que vai dar o seguinte campo magnético resultante:
que simplificada dá:
Passo 3
b) Como já temos a expressão para para uma espira percorrida por num ponto arbitrário, só temos que tomar cuidado com a direção do campo resultante produzido pela corrente da espira superior e também com a distância ’ do plano dela até o ponto .
Nesse caso, para a corrente de cima, a direção e sentido de seu campo resultante estarão ao longo de e está a uma distância do plano da espira superior. Substituindo isso na expressão do final do Passo 2, vamos ter:
Portanto, o campo magnético quando tivermos as duas espiras será:
Passo 4
c) Quando , o primeiro termo entre parênteses é igual ao segundo, o que vai dar