Considere uma espira quadrada de lado percorrida por uma corrente estacionária no sentido anti-horário, e sujeita a um campo magnético externo estacionário e uniforme . A espira se encontra no plano , conforme a figura.
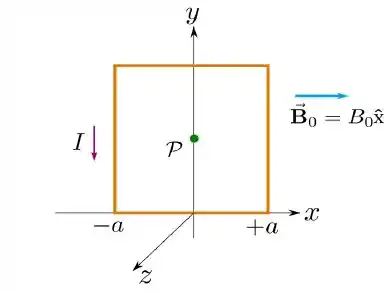
Calcule as forças sobre o lado horizontal superior do quadrado e sobre o lado vertical à direita do quadrado, exercidas pelo campo magnético externo.
Determine o momento de dipolo magnético associado à espira e calcule o vetor torque que o campo externo exerce sobre a mesma.
Determine o campo magnético produzido pela espira no seu centro .
Passo 1
Calcule as forças sobre o lado horizontal superior do quadrado e sobre o lado vertical à direita do quadrado, exercidas pelo campo magnético externo.
A força magnética sobre um fio condutor é dada por:
No caso de um condutor retilíneo, podemos reescrever a expressão acima da seguinte forma:
Onde tem a mesma direção e sentido da corrente, e o módulo é igual ao tamanho do condutor. Logo:
Assim, sabendo que o campo magnético é dado por , teremos:
Passo 2
Determine o momento de dipolo magnético associado à espira e calcule o vetor torque que o campo externo exerce sobre a mesma.
O momento de dipolo magnético é dado por:
Onde o módulo de é igual à área da espira, e a direção e sentido do vetor são dados a partir do sentido da corrente. Nesse caso, como a corrente está no sentido anti-horário, utilizando a regra da mão direita, o vetor será dado por:
Assim, o momento de dipolo magnético será:
Passo 3
O torque magnético é dado por:
Portanto:
Passo 4
Determine o campo magnético produzido pela espira no seu centro .
Por conta da simetria do problema, os campos magnéticos produzidos por cada lado da espira deverão ser iguais. Como o campo magnético da espira é a soma vetorial dos campos magnéticos produzidos por cada lado, portanto:
Ok, então, vamos começar calculando o campo magnético gerado por apenas um dos lados.
Nesse caso, vamos utilizar o lado horizontal inferior da espira, que está sobre o eixo .
O campo magnético pode ser calculado através da lei de Biot-Savart, dada por:
Então vamos analisar graficamente a situação aqui e ver o que podemos tirar disso, beleza?
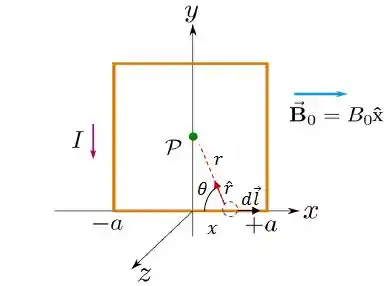
Daqui podemos tirar que:
Onde:
Logo:
Agora podemos partir pra brincadeira.
Passo 5
Como e , teremos:
Esse é o tipo de integral que você olha e dá aquela bugada na cabeça, mas como é uma integral que aparece muitas vezes nesse tipo de problema, a resposta dela costuma estar no formulário.
Então, nesses casos, vá no formulário e dê uma olhada pra ver se a resposta está por lá. No caso dessa prova, a resposta da integral está no formulário, e é dada por:
Substituindo os valores, teremos:
Agora é só ir arrumando esse cara na base da calma:
Conforme falamos lá em cima:
Logo:
Resposta