A figura abaixo mostra um circuito formado por dois trechos semicirculares de raios e e dois trechos retos. Uma corrente percorre o circuito no sentido indicado na figura. Calcule o campo magnético no ponto .
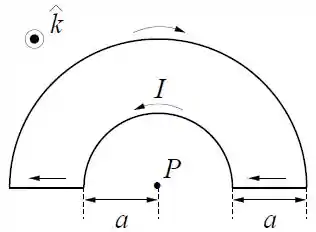
Passo 1
Calcule o campo magnético no ponto .
O primeiro passo é dividir esse problema em 4 partes, onde calcularemos o campo magnético gerado por cada fio (arco maior, arco menor e fios retilíneos) através da Lei de Biot-Savart, dada por:
Como a corrente é uniforme, podemos reescrever a lei dessa forma:
Lembrando que sempre está na direção e sentido da corrente.
Passo 2
Vamos nessa!
- Fios retilíneos:
- Arco maior:
- Arco menor:
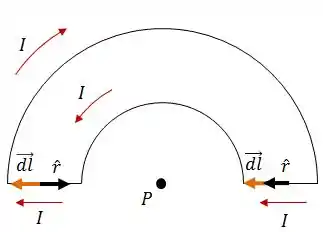
Nos dois fios retilíneos, e são colineares. Isso significa que, em ambos os casos:
Logo, para ambos:
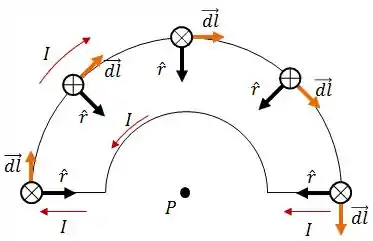
Para o arco maior, , , onde o vetor é positivo quando no sentido anti-horário.
Assim, para o arco maior:
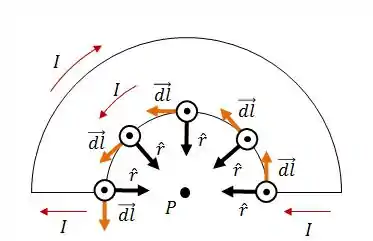
Para o arco menor, , .
Assim, para o arco menor:
Assim, o campo magnético total gerado no ponto será:
Resposta