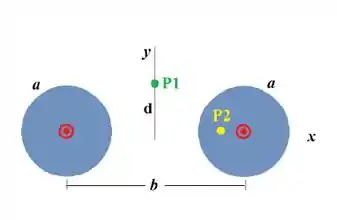
Os dois fios retos, infinitos e paralelos ao eixo z têm raios a. Seus eixos, contidos no plano e também paralelos ao eixo, estão afastados conforme mostra a Figura. São percorridos por correntes iguais, uniformemente distribuídas nos seus interiores com densidade no sentido Determine o vetor campo magnético nos pontos:
- de coordenada .
- de coordenada .
- O vetor força (por unidade de comprimento) exercida pelo fio da esquerda sobre o fio da direita, de .
Em seguida, suponha que as correntes totais estejam concentradas nos respectivos eixos e determine:
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Vamos desenhar os campos e para entendermos melhor:
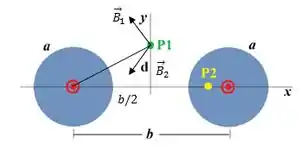
Por simetria temos que as componentes verticais dos campos se cancelam e sobram apenas as componentes horizontais. Assim o campo resultante nesse ponto é:
O ângulo é o ângulo entre o eixo e a distância entre o ponto e o fio.
A distância do ponto até os fios é:
Então pela lei de Ampére temos:
E a corrente é:
E o campo no ponto fica:
Passo 2
Letra (b):
Agora não temos mais simetria, então precisamos encontrar os dois campos. Vamos começar pelo desenho:
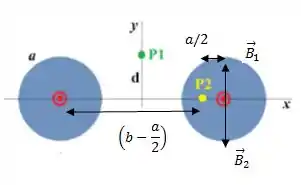
Vamos começar pelo campo que é na direção vertical para cima. A distância dele até o ponto é e pela lei de Ampére podemos encontrar o campo:
Para o campo temos que a distância dele até o ponto é e aplicando novamente a lei temos:
E por fim o campo total é a soma dos dois campos:
Tranquilo? Vamos para o último item?
Passo 3
Letra (c):
Supondo as correntes totais concentradas nos respectivos eixos, tem-se:
Agora vamos usar os resultados obtidos nos itens anteriores, usando a lei de Ampére e sabendo que agora a distância entre os fios é :
Beleza?
Pronto pra próxima questão? =)