Halliday - Vol. 3 – 9º edição – Capítulo 29 – Seção 3 – Exercício 41
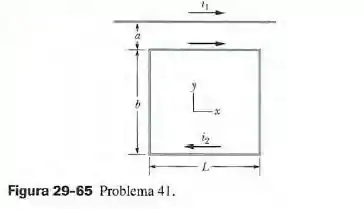
(Capítulo 29.3 – Exercício 41) Na figura 29-65, um fio retílíneo longo conduz uma corrente e uma espira retangular conduz uma corrente . Suponha que , e . Em termos dos vetores unitários, qual é a força a que está submetida a espira?
Passo 1
Eaeee pessoal!
Se liga: aqui queremos encontrar a força magnética que a espira está sendo submetida
Temos que
Nesse exercício, podemos calcular os módulos das forças exercidas sobre os lados da espira paralelos ao fio longo usando a expressão mostrada acima. No entanto, as forças exercidas sobre os lados perpendiculares teriam que ser calculadas através de integrais do tipo:
Entretanto, por conta da simetria do problema, as forças exercidas sobre os lados perpendiculares ao fio longo se cancelam.
Então vamos calcular apenas para os lados paralelos, ok?
Passo 2
Para os lados paralelos, temos:
E aponta na direção do fio. Assim, na notação de vetores unitários:
Sucesso!
Resposta
A força é: