Força e Torque sobre uma Espira, Lei de Biot-Savart
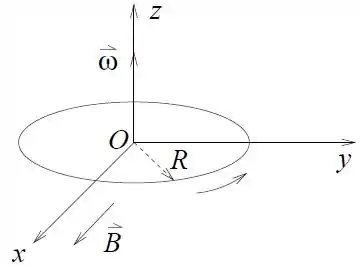
Um anel fino de raio , carregado com densidade linear de carga , gira em torno de um eixo que passa pelo centro com uma velocidade angular , conforme a figura.
Atua na região um campo magnético externo homogêneo .
- Calcule a corrente associada ao movimento do anel em função de , e . Qual é o sentido da corrente?
- Calcule o vetor torque que o campo externo exerce sobre o anel.
- Calcule o campo magnético produzido pelo anel no seu centro.
Passo 1
- Calcule a corrente associada ao movimento do anel em função de , e . Qual é o sentido da corrente?
- Calcule o vetor torque que o campo externo exerce sobre o anel.
- Calcule o campo magnético produzido pelo anel no seu centro.
A definição de corrente é a seguinte:
Em uma volta inteira, . Além disso, . Logo:
Como as cargas estão se movimentando devido à velocidade , a corrente tem o mesmo sentido de rotação do anel.
Passo 2
O torque magnético sobre uma espira é dado por:
Onde .
O vetor é perpendicular ao plano da espira e nós encontramos o seu sentido usando a regra da mão direita no sentido da corrente. Assim:
Agora é só calcular o torque e ser feliz.
Substituindo o que achamos para a corrente no passo 1:
Passo 3
Nesse caso, vamos ter que usar a lei de Biot-Savart:
Como se trata de uma espira circular e estamos querendo calcular o campo magnético no seu centro, vai apontar na direção radial para dentro da espira e da corrente na figura do enunciado.
Portanto, o produto escalar apontará na direção .
Voltando para a fórmula:
Onde .
Resposta
-
; A corrente tem o sentido do anel.