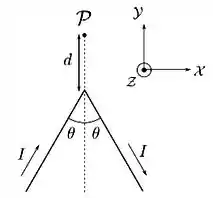
Um fio condutor fino, retilíneo e infinito é dobrado de forma que suas duas metades formam um ângulo entre si, como mostrado na figura abaixo. O fio é atravessado por uma corrente estacionária de intensidade no sentido indicado. Utilizando a lei de Biot-Savart e o sistema de coordenadas indicado na figura, determine o campo magnético (módulo, direção e sentido) no ponto mostrado na figura, localizado a uma distância do ponto de dobra, ao longo da reta bissetriz do ângulo . Analise e interprete o caso limite .
Passo 1
Pela simetria do problema, vemos que o campo magnético resultante produzido por cada metade do fio deve ser o mesmo no ponto . Assim sendo, vamos considerar apenas uma das metades e multiplicado o resultado final por . Escolhemos a metade direita do fio.
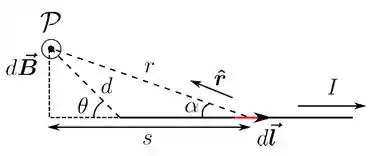
Vamos olhar para o sistema em um novo ângulo: giramos a figura no sentido anti-horário para que a metade direita do fio fique na horizontal. Consideramos, agora, um elemento de comprimento infinitesimal , orientado no sentido da corrente. Esse elemento está a uma distância da projeção de pela reta que passa pelo fio, como podemos ver na figura.
Passo 2
Pela lei de Biot-Savart, a contribuição de para o campo magnético em é dada por:
Pela figura, vemos que e , de modo que:
Passo 3
Assim, o campo magnético resultante será:
Aqui, estamos considerando apenas a metade direita do fio e incluímos o fator dois para contar as duas partes.
Bem... e agora? No formulário da prova, temos a solução da seguinte integral:
Se fizermos e , conseguimos usar a fórmula acima para resolver a integral. Temos:
Passo 4
Para , vemos que:
que nada mais é que o campo produzido por um fio retilíneo e infinito situado a uma distância do ponto . Isso era esperado, pois para , o fio não está dobrado e é retilíneo e infinito.