PARTE 1:
A figura abaixo mostra duas espiras planas: a espira 1 é circular, de raio ; a espira 2 é formada por duas semicircunferências, uma de raio e outra de raio , interligadas por dois segmentos retilíneos.
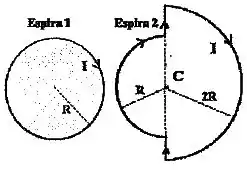
Correntes de mesma intensidade circulam pelas duas espiras.
Seja o módulo do campo magnético gerado pela espira 1 em seu centro, e o módulo do campo magnético gerado pela espira 2 em seu centro (ponto C). Considerando que as espiras estão muito afastadas uma da outra, calcule a razão .
Passo 1
Seja o módulo do campo magnético gerado pela espira 1 em seu centro, e o módulo do campo magnético gerado pela espira 2 em seu centro (ponto C). Considerando que as espiras estão muito afastadas uma da outra, calcule a razão .
Espira 1:
O campo magnético gerado pela espira a uma distância do centro da mesma, sobre o seu eixo de simetria, é dado por:
No centro da espira, , logo:
Passo 2
Espira 2:
Para calcular o campo gerado por essa espira, vamos usar a Lei de Biot-Savart, dada por:
Para isso, vamos dividir a espira em 4 segmentos: dois segmentos retilíneos e duas semicircunferências. Para cada segmento, vamos posicionar os vetores (sempre no tangente ao fio e com o mesmo sentido da corrente) e (sempre apontando para o ponto onde estamos calculando o campo magnético).
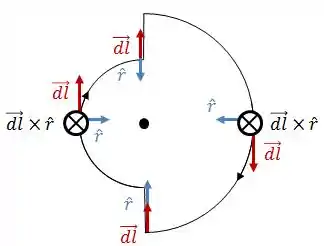
Para os segmentos retilíneos, e são paralelos, logo, . Assim, esses segmentos não geram campo magnético no centro da espira.
Em ambos os segmentos semicirculares, aponta para o dentro do plano da página, assim, o ponto eles irão se somar, já que possuem o mesmo sentido. Dessa forma:
Para a semicircunferência menor, , e para a semicircunferência maior , onde . Dessa forma:
Passo 3
Finalmente, a razão será:
Resposta