Um fio infinitamente longo transportando uma corrente é dobrado conforme a figura, sendo que a parte semicircular está contida no plano .
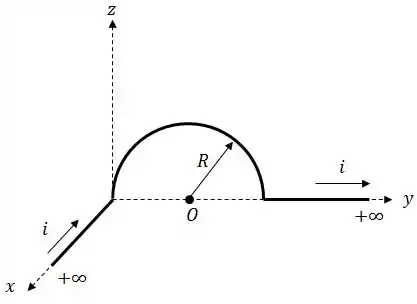
Calcule no ponto :
O vetor campo magnético devido às partes retas do fio;
O vetor campo magnético devido à espira semicircular;
O campo magnético total;
A força que atua sobre uma carga com velocidade no ponto ;
Passo 1
O vetor campo magnético devido às partes retas do fio;
Para calcular o campo magnético, vamos precisar da lei de Biot-Savart, dada por:
Onde o vetor tem a mesma direção e sentido da corrente.
Vamos fazer uma parte retilínea de cada vez, ok?
- Fio no eixo :
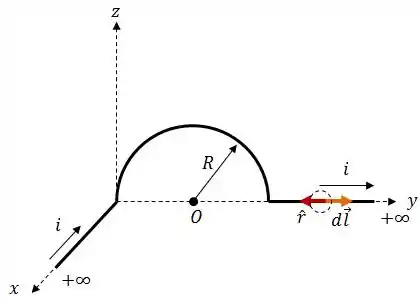
Aqui podemos ver que os vetores são anti-paralelos, logo:
Passo 2
- Fio no eixo :
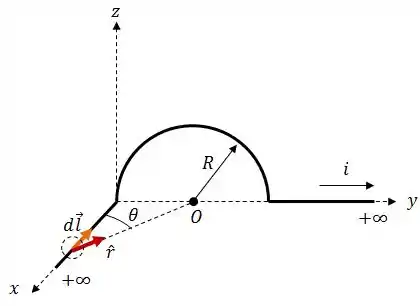
Da figura podemos tirar que:
Substituindo isso na expressão da lei de Biot-Savart, teremos:
Se você olhou pra essa integral e não faz ideia de como ela é resolvida, o próximo passo vai te ensinar a resolver a integral.
Passo 3
Ok, vamos voltar naquela integral:
Esse cara é resolvido a partir de uma substituição trigonométrica:
Logo:
Lembrando que , podemos reescrever a expressão acima como:
A partir da substituição que fizemos, podemos dizer que:
Colocando isso em um triângulo retângulo, podemos ver que:
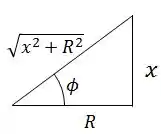
Sendo assim:
Esse é o tipo de integral que vira e mexe aparece nesse tipo de questão. Algumas vezes o próprio problema dá a resposta dessa integral, ou ela pode estar no seu formulário, mas se não estiver, agora você sabe calcular.
Passo 4
O vetor campo magnético devido à espira semicircular;
Novamente, vamos recorrer à lei de Biot-Savart:
Vamos analisar graficamente esse cara:
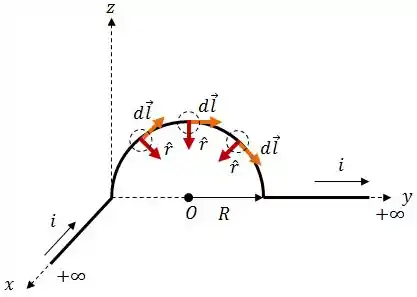
Aqui é possível ver que, para qualquer ponto que analisarmos:
Logo:
Passo 5
O campo magnético total;
O campo magnético total será dado por:
Passo 6
A força que atua sobre uma carga com velocidade no ponto ;
A força magnética sobre a carga é dada por:
Resposta