Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Biot-Savart Geral

Ver Teoria
Exercício 571234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556585960616263646566676869707172737475767778

Enunciado

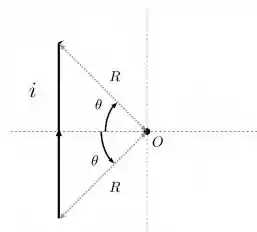
A figura ao lado representa uma espira composta por uma seção incompleta de circunferência de raio R , cujas extremidades são unidas por um segmento reto. A espira é percorrida por uma corrente i constante e uniforme, cujo sentido está representado na Figura através das setas. Sabendo que o ângulo θ   =   45 ° = π / 4   e utilizando explicitamente a lei de Biot-Savart, calcule:

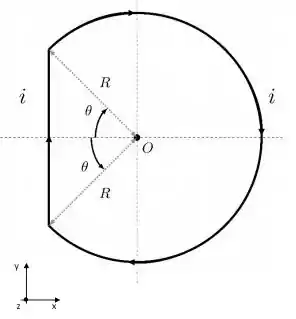
a) O vetor campo magnético B → gerado pela seção incompleta de circunferência no ponto O.

b) O vetor campo magnético B → gerado pela seção reta no ponto O.

Passo 1

L e t r a   A :

Para começar, temos que fixar o que queremos resolver no problema do item A : queremos encontrar o campo magnético B → c i r da seção circular...

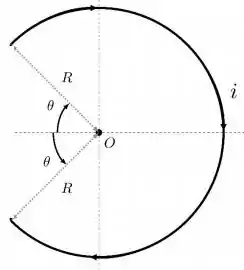
De acordo com Biot-Savart, podemos encontrar o campo elétrico através da fórmula...

B → c i r = μ 0 i 4 π   ∫ d l → × r → r 2

Onde d l → é o vetor de direção da corrente e r → é o vetor de distância da corrente ao ponto onde se está medindo o campo elétrico (centro)...

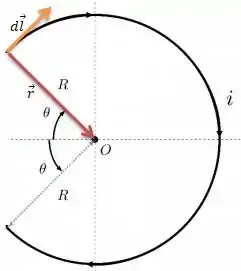
Ora... O módulo do produto vetorial é...

d l → × r → = d l sin ⁡ ϕ

Onde ϕ é o ângulo entre o vetor d l → e r → que é ϕ = 90 ° . Só que pela regra ad mão direita, o sentido do produto vetorial d l → × r → é para dentro ( - z ^ )...

d l → × r → = - d l → × r →   z ^     →

d l → × r → = - d l sin ⁡ 90 °   z ^     →

Então...

d l → × r → = - d l   z ^

Ou seja, pela regra de Biot-Savart...

B → c i r = - μ 0 i 4 π   ∫ d l   R 2   z ^   →

B → c i r → = - μ 0 i 4 π R 2   ∫ d l   z ^   →

Só que quem é a integral de d l ???

Passo 2

Ora... A integral de d l é o comprimento da curva...

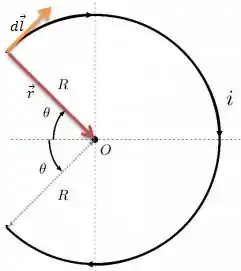
No caso, a curva é quase uma circunferência inteira de raio R , então o comprimento seria...

C = 2 π R

Mas no nosso caso, a curva é apenas 3 / 4 de comprimento...

∫ d l = 3 4   2 π R   →

∫ d l = 3 2 π R

Então...

B → c i r = - μ 0 i 4 π R 2   ∫ d l   z ^   →

B → c i r = - μ 0 i 4 π R 2   3 2 π R   z ^   →

B → c i r = - 3 μ 0 i 8 R   z ^  

Passo 3

L e t r a   B :

Nesse item temos que buscar campo magnético gerado pela seção reta B r e t a ...

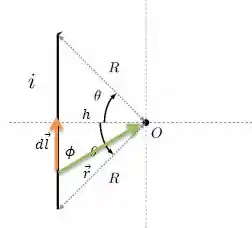
O campo B → r e t a feita por esse fio de corrente no ponto O é para dentro da tela na direção - z ^ . Então...

B → r e t a = - B r e t a   z ^

De acordo com a teoria podemos encontrar o valor desse campo magnético pela fórmula:

B r e t a = μ 0 i 4 π ⋅ ∫ d l r 2 sin ⁡ ϕ

Muita calma nessa hora! r sempre vai ser a distância ente o trechinho de corrente ao ponto onde se ta medindo d B . ϕ já vai ser o ângulo entre d l e r :

Pode memorizar isso brother, pois você vai utilizar na sua prova!

Passo 4

O valor da distância desse segmento de reta e o ponto O é...

h = R cos ⁡ θ = R cos ⁡ 45 °   →

h = R   2 2

Então...

sin ⁡ ϕ = h r

De modo que...

B r e t a = μ 0 i 4 π ⋅ ∫ d l r 2 sin ⁡ ϕ   →

B r e t a = μ 0 i 4 π ⋅ ∫ d l r 2 h r   →

B r e t a = h μ 0 i 4 π ⋅ ∫ d l r 3   →

Só que por trigonometria...

r 2 = l 2 + h 2

De modo que...

B r e t a = h μ 0 i 4 π ⋅ ∫ d l l 2 + h 2 3 / 2   →

Essa integral é igual a...

B r e t a = h μ 0 i 4 π ⋅ l h 2 l 2 + h 2 1 / 2 l i n f e r i o r l s u p e r i o r   →

Só que no nosso caso, repare que l varia de...

l 2 = R 2 - h 2   →

l i n f e r i o r = - R 2 - h 2             a o             l s u p e r i o r = R 2 - h 2

Então...

B r e t a = h μ 0 i 4 π ⋅ l h 2 l 2 + h 2 1 / 2 - R 2 - h 2 R 2 - h 2   →

Substituindo os limites...

B r e t a = h μ 0 i 4 π ⋅ R 2 - h 2 h 2 R 2 - h 2 + h 2 1 / 2 + R 2 - h 2 h 2 R 2 - h 2 + h 2 1 / 2   →

B r e t a = h μ 0 i 2 π ⋅ R 2 - h 2 h 2 R 2 1 / 2   →

Como h = R   2 2 ...

B r e t a = h μ 0 i 2 π ⋅ R 2 - 1 2 R 2 1 2 R 2 R   →

B r e t a = h μ 0 i 2 π ⋅ R 2 1 2 R 2 R   →

B r e t a = R   2 2 μ 0 i 2 π ⋅ 2 R 2 R 2 R   →

B r e t a =   μ 0 i 2 π ⋅ 1 R   →

Então, podemos concluir que...

B r e t a =   μ 0 i 2 π R  

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

14- Uma partícula com carga 6.40 × 10 - 19C se desloca ao longo de uma órbita circular com raio igual a 4.68m m , em virtude da força oriunda de um campo magnético de módulo 1.65T , cuja direção é per
15- Um elétron no ponto A da Figura 27.46 possui velocidade v 0 igual a 1.41 × 10 6m / s . Determine: ( a ) o módulo, a direção e o sentido do campo magnético que obriga o elétron a descrever uma órbi
16- Repita o Exercício 27.15 para o caso no qual a partícula é um próton em vez de um elétron.
Dois fios longos estão no plano x y e conduzem correntes no sentido positivo do eixo x . O fio 1 está em y = 10,0c m e conduz uma corrente de 6,00A ; o fio 2 está em y = 5,00c m e conduz uma corrente
Na figura 29-63, cinco fios paralelos longos no plano x y estão separados por uma distância d = 8,00c m , têm 10,0m de comprimento e conduzem correntes iguais de 3,00A para fora do papel. Em termos do