Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Biot-Savart Geral

Ver Teoria
Exercício 211234567891011121314151617181920222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778

Enunciado

UFRJ – Física 3 – 2019.2 – P2

4 . Considere as representações e expressões para os seguintes campos vetoriais ( C é uma constante positiva):

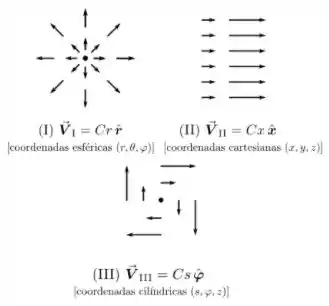
Qual(is) de tais campos nitidamente não pode(m) ser campo(s) magnético(s)?

( a ) Somente I e I I

( b ) Somente I e I I I

( c ) Somente I I e I I I

( d ) Nenhum deles pode ser campo magnético

( e ) Todos podem ser campos magnéticos

( f ) Somente I

( g ) Somente I I

( h ) Somente I I I

Passo 1

Vem comigo para gente destruir esse problema.

Vamos avaliar cada campo vetorial separadamente e ver se ele pode ser associado a algum campo magnético.

Passo 2

Vamos começar com I .

Esse campo vetorial representaria o campo de uma “carga” ou deum único polo magnético, mas aé onde se sabe não se existe mono polos magnéticos, logo esse campo vetorial não é um campo magnético.

Passo 3

Agora vamos analisar I I .

Como podemos ver pela figura o campo vetorial cresce com a distância x e o campo magnético cai com a distância ou ele é constante, logo esse campo vetorial não pode ser magnético.

Passo 4

E por último temos I I I .

Se olharmos esse campo podemos associar ao campo de um fio com corrente pela forma “circular”, e caso a analise seja feita dentro do fio, temos que o campo poderá aumentar como mostrado na figura.

Logo esse pode representar um campo magnético.

Portanto, os únicos campos vetoriais que NÃO representa um campo magnética é somente I e II, letra (a).

Resposta

( a ) Somente I e II.

Exercícios de Livros Relacionados

14- Uma partícula com carga 6.40 × 10 - 19C se desloca ao longo de uma órbita circular com raio igual a 4.68m m , em virtude da força oriunda de um campo magnético de módulo 1.65T , cuja direção é per
15- Um elétron no ponto A da Figura 27.46 possui velocidade v 0 igual a 1.41 × 10 6m / s . Determine: ( a ) o módulo, a direção e o sentido do campo magnético que obriga o elétron a descrever uma órbi
16- Repita o Exercício 27.15 para o caso no qual a partícula é um próton em vez de um elétron.
Dois fios longos estão no plano x y e conduzem correntes no sentido positivo do eixo x . O fio 1 está em y = 10,0c m e conduz uma corrente de 6,00A ; o fio 2 está em y = 5,00c m e conduz uma corrente
Na figura 29-63, cinco fios paralelos longos no plano x y estão separados por uma distância d = 8,00c m , têm 10,0m de comprimento e conduzem correntes iguais de 3,00A para fora do papel. Em termos do