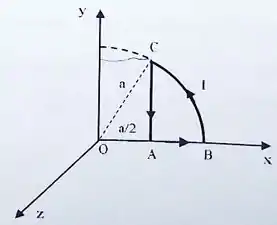
Considere a espira da figura formada pelo arco de circunferência centrado em e raio , pelo segmento de comprimento sobre o eixo e pelo segmento paralelo ao eixo . A espira é percorrida por uma corrente de intensidade com sentido mostrado na figura (anti-horário).
Nestas condições, utilizando explicitamente a Lei de Biot-Savart e justificando as suas afirmações, determine:
(a) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
(b) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
(c) O campo magnético (módulo, direção e sentido) na origem devido ao arco .
(d) O campo magnético total (módulo, direção e sentido) na origem .
Passo 1
Bom, vamos lá. Para começar, vamos relembrar o que a lei de Biot-Savart nos diz. Temos:
onde o vetor aponta na direção da corrente e aponta para onde queremos medir o campo, respectivamente. Além disso, é a distância até o ponto no qual o campo será medido. Beleza? Vamos adiante.
Passo 2
No item (a), queremos medir o campo na origem gerado pelo segmento . Vamos olhar para a figurinha abaixo.
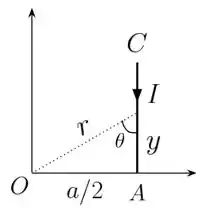
Bem, da figura, podemos concluir que a distância à origem de um elemento de corrente infinitesimal é dada por:
Vamos calcular também o seno de , para quando fizermos o produto vetorial . Temos:
Pra finalizar, vemos que é, na verdade, .
Passo 3
Agora podemos reescrever a equação de Biot-Savart com as informações que a gente obteve acima. Saca só:
O sentido e direção de podem ser obtidos pela regra da mão direita! Bem, como aponta para baixo e tem a direção da reta tracejada da figura, apontando para a origem, irá apontar para dentro da página, ou seja, no sentido negativo do eixo .
Passo 4
Por fim, para obter , integramos a equação acima. Lembrando que varia de até , que é o comprimento de . Temos:
Agora precisamos resolver essa integral! Para isso, fazemos a seguinte substituição de variáveis:
Para , e para , .
A integral resultante vai ser:
Lembrando que:
Logo:
Substituindo os limites de integração:
Chegamos a reposta final:
Botando a direção
Passo 5
Agora, vamos para o item (b). Nesse caso, os vetores e tem a mesma direção. Isso significa que , pois o seno do ângulo entre eles é nulo. Isso significa que
Passo 6
Agora só falta calcular a contribuição do arco , certo? Estamos quase lá! Nesse caso, a distância à origem é sempre constante e igual a . Além disso, o ângulo entre e é reto. Pela regra da mão direita, o campo na origem aponta para fora, no sentido positivo de .
Temos:
Botando a direção
Passo 7
O campo magnético total na origem será:
Resposta
(a)
(b)
(c)
(d)