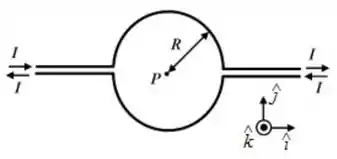
Determine o módulo, a direção e o sentido do campo magnético resultante no ponto da figura abaixo, que representa dois fios finos isolados conduzindo corrente . Considere o ponto localizado no centro das duas semi-circunferências e na direção dos fios retilíneos
(a)
(b)
(c)
(d)
(e)
Passo 1
Olhando para o fio de cima, vemos que pela regra da mão direita que o campo magnético tem que apontar para dentro da página, ou seja, na direção .
Olhando para o fio de baixo, vemos que o seu campo também aponta para dentro da página.
Assim já concluímos que o campo é não nulo e aponta na direção !
Passo 2
Agora vamos calular o campo gerado pelo fio de cima usando Biot-Savart
Onde é um elemento de comprimento do fio e é o vetor unitário que aponta desse elemento de comprimento até o ponto (onde queremos calcular o campo).
Vemos que nessas partes retas está na direção e que o vetor também, o que significa que o produto vetorial na lei de Biot-Savart será nulo e a contribuição desses pedaços retos de fio será nula.
Agora temos que nos preocupar com a parte do fio que tem formato de semi-circulo. Nessa parte o elemento infinitesimal de comprimento será
Onde é o vetor unitário tangente ao semi-circulo.
Já o vetor aponta na direção , apontando do círculo para o ponto . De forma que o produto vetorial
Dessa forma o campo do fio superior é dado por
Da mesma forma o campo gerado pelo fio de baixo é dado por
Assim
Resposta
(b)