UFRJ – Física 3 – 2020.2 – PF – M.Escolha
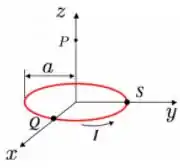
. Uma espira condutora circular de raio é posicionada sobre o plano de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ela transporta uma corrente estacionária de intensidade , no sentido indicado. Considere um elemento de comprimento infinitesimal desta espira, localizado no ponto e orientado no sentido da corrente. Qual é o campo magnético produzido por este elemento em um ponto localizado sobre o eixo ?
Escolha uma opção:
Passo 1
Vem comigo que a gente resolve essa juntos!
Um elemento de comprimento tem uma contribuição para o campo magnético em .
Só que campo magnético é um vetor então realiza uma contribuição de . Para encontrarmos vamos usar a lei de Biot-Savart, dada por:
Onde é o versor que aponta na direção entre e nesse caso e é a distância entre esses pontos. Então vamos atrás do que queremos usando essa lei.
Passo 2
Então o que temos de principal para calcular na lei de Biot-Savart é o produto vetorial e sabermos quem é .
O versor pode ser dado da seguinte forma:
O vetor que aponta de para , pode ser escrito da seguinte forma:
Então nosso produto vetorial é dado por:
Como é o vetor elemento de comprimento em e ele é tangente a trajetória circular, temos que , assim:
Passo 3
O como já falamos é a distância entre o elemento e , podemos achar essa distância usando Pitágoras ao nosso favor, olhando a figura temos que:
Passo 4
Juntando tudo temos o seguinte:
Então nossa alternativa correta é a letra .