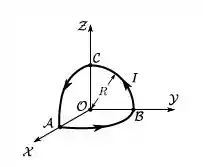
Um circuito fino, percorrido por uma corrente estacionária de intensidade , é constituído por 3 quartos de circunferência. Todos esses 3 arcos têm raio e situam-se em 3 diferentes planos ortogonais, com centro comum com a origem O de um sistema de coordenadas cartesianas, conforme mostra a figura abaixo. Qual é o campo magnético produzido por este circuito na origem O?
Passo 1
Se liga! Pela regra da mão direita podemos dizer que o segmento localizado no plano , gera um campo orientado no sentido positivo da direção . Da mesma forma, os segmentos localizados nos planos e produzem campos nos sentidos positivos das direções, e , respectivamente.
Passo 2
Como todos os segmentos possuem o mesmo tamanho e estão a mesma distância do ponto, podemos simplesmente calcular a intensidade do campo de um segmento e repetir para o restante.
Pela lei de Bio-Savart, temos que
Como o segmento é de uma circunferência, temos
Como falamos no passo 1, podemos imprimir as direções. Gerando que
Encontramos que a resposta é o item (a).