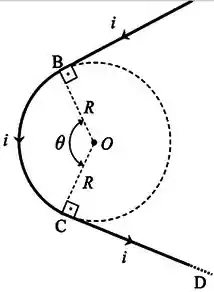
Na figura abaixo temos dois fios retilíneos semi-infinitos e , conectados a um fio curvo que é um segment circular de raio e abertura angular . Todos os fios pertencem ao plano da página e são percorridos por uma corrente elétrica constant . Nestas condições,
- Escreva a equação da lei de Biot-Savart em sua forma vetorial, identificando numa figura esquemática todos os elementos inerentes a tal equação
- Calcule o modulo do campo magnético total em , expressando seu resultado em termos de , e .
- Qual a direção e o sentido (com relação ao plano da página) do vetor campo magnético total em ?
Passo 1
Letra (a). A Lei de Biot-Savart determina o campo magnético gerado por cada pedacinho de um fio em termos vetoriais. Por isso, quando o fio tem um formato mais maluco (como é o caso da questão), temos de recorrer a essa lei.
Um caso específico da lei de Biot-Savart é a lei de Ampère mas ela se aplica apenas a fios retilíneos e infinitos. Enfim, vamos representar isso esquematicamente, como a questão pede:
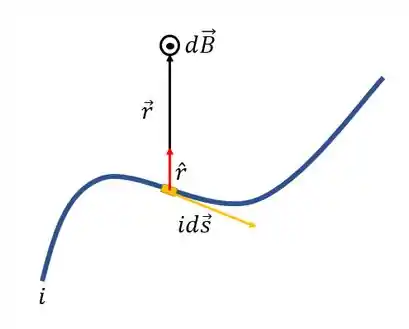
Gostou do desenho? A galera da NASA que fez pra mim 😉
é a componente de campo gerada pelo pedacinho de fio, onde passa a corrente i, na direção (vetor unitário). A distância entre esse pedacinho de fio e o ponto onde queremos analisar o campo magnético gerado vale , o “r” com chapeuzinho é o vetor unitário ok? Então:
Onde, lembrando,
Passo 2
Letra (b). Temos então de integrar três pedaços diferentes. Vamos começar aqui com a primeira parte: o pedaço !
Temos nessa situação o seguinte:
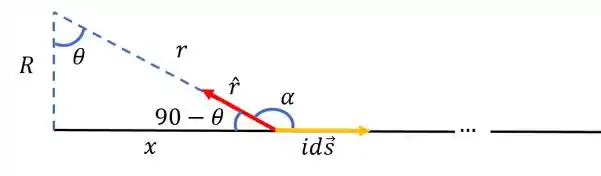
Pela figura:
Só que
E então
E assim
Além disso
Substituindo na equação:
Temos então de expressar em função de . Na verdade, podemos notar que:
Substituindo isso, resta integrar para variando de a :
O campo gerado por esse pedaço aponta para cima, no ponto O, saindo da folha de papel. Os mesmos cálculos e a mesma coisa acontece quando tomamos o campo :
Queremos, na verdade, o valor de:
Sabemos uma parte dessa soma:
Resta então calcular o campo magnético gerado pela parte redonda. Lembre-se: consideramos campos positivos quando eles apontam para fora da página, ok?
Passo 3
Letra (b). Continuação. Indo para a parte redonda, o arco , temos que os vetores e formarão um ângulo de em cada pedaço do fio. Além disso: . Ou seja:
Assim, esse vetor representa um vetor que aponta para fora da página.
A integração nessa situação é ainda mais direta:
Assim, somando todos os campos, chegamos até a resposta final:
Passo 4
Letra (c). Assim, todos os campos magnéticos gerados por diferentes partes do fio contribuem para que o campo magnético aponte para fora da página.
Resposta
Letra (a).
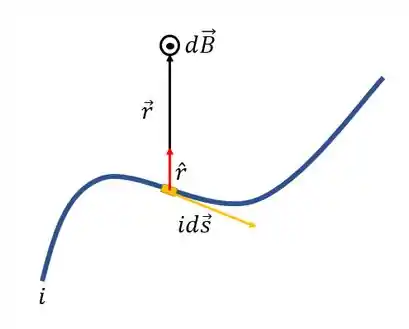
Letra (b).
Letra (c).
Para fora, saindo, do plano da página.