Lei de Biot Savart
Um circuito é formado por duas semicircunferências de raios e , como é mostrado na figura abaixo.
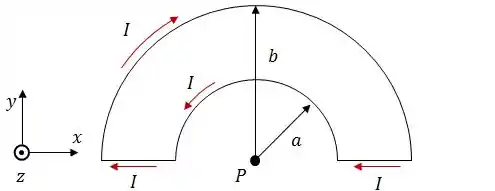
O vetor campo magnético produzido pelas correntes do fio no ponto P é dado por:
Passo 1
Em problemas como esse, quem pode nos ajudar é a lei de Biot-Savart, dada por:
Onde o vetor tem a mesma direção e sentido da corrente:
Então vamos começar dividindo esse problema em 4 partes e calcular o campo magnético gerado por cada segmento dessa espira.
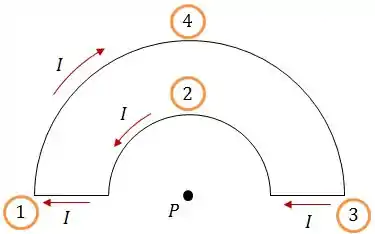
No final das contas:
Passo 2
Vamos começar pelos fios retilíneos 1 e 3. Neles vamos ver como se comportam os vetores e .
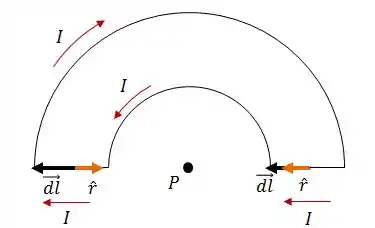
Em ambos os fios retilíneos, os vetores e são paralelos ou antiparalelos, logo:
Passo 3
Agora vamos olhar para o arco menor, ok?
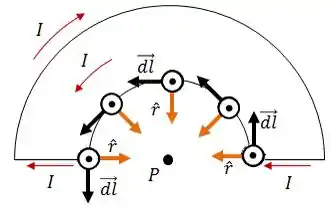
Daqui podemos tirar que:
Logo:
Passo 4
Por último, vamos para o arco maior:
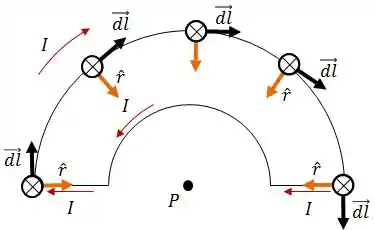
Daqui podemos tirar que:
Logo:
Finalmente:
Resposta