A Fig. 1 mostra um segmento retilíneo de comprimento de um fio que conduz corrente no sentido . O centro do segmento está na origem. Um ponto está sobre o eixo à distância da origem.
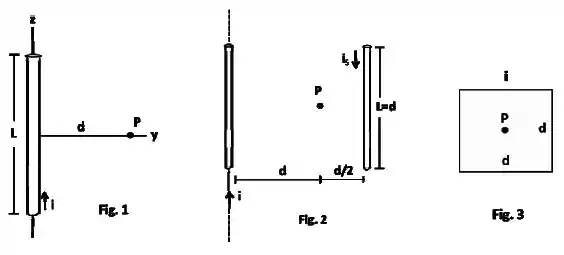
Mostre, utilizando explicitamente, a lei de Biot-Savart, que o vetor campo magnético em devido a todo o segmento é dado por:
Considere agora a Fig. 2 que mostra um ponto à distância de um fio infinito com corrente . O módulo do campo magnético devido ao fio infinito no ponto é dado por . A figura mostra também um segmento retilíneo com corrente antiparalela a . O segmento tem comprimento e está simetricamente disposto em relação ao ponto e dista dele.
Quanto deve valer a corrente para que o módulo do campo total em seja ?
Considere agora a Fig. 3 que mostra uma espira quadrada de lado que conduz uma corrente de valor . A espira é centrada em .
Utilizando o resultado do item , calcule o módulo do campo magnético em em função de , e . A corrente deve circular na espira no sentido horário ou anti-horário para que o campo em tenha sentido saindo da página?
Passo 1
Mostre, utilizando explicitamente, a lei de Biot-Savart, que o vetor campo magnético em devido a todo o segmento é dado por:
Beleza, vamos nessa!
A lei de Biot-Savart é dada por:
Vamos começar pegando um ponto aleatório do fio para analisar esses vetores e .
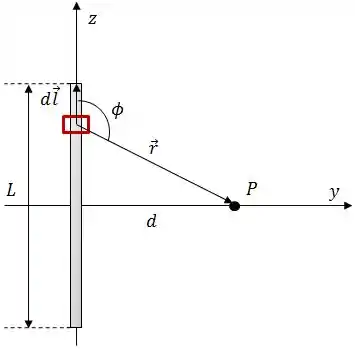
Onde:
Substituindo na lei de Biot-Savart, onde vai variar entre e :
Onde .
Eu sei que nesse momento você olha pra essa integral e bate aquele desespero de leve... aquela lágrima escorre de boa e tal... mas não tema!
Se você tiver que resolver esse tipo de integral, a resposta dela deve estar no seu formulário. Então é só ir lá e dar uma conferida.
Substituindo os valores:
Passo 2
Quanto deve valer a corrente para que o módulo do campo total em seja ?
Opa! Beleza!
Dados os sentidos das correntes e , usando a regra da mão direita, você consegue ver que elas vão se somar no ponto ?
Isso significa que o campo magnético total ali vai ser a soma desses dois caras, onde o campo resultante vai estar entrando na página.
O campo magnético gerado pela corrente , no ponto , é dado pelo problema.
No ponto , o campo magnético gerado pela corrente é dado pela fórmula que encontramos na letra ... a única diferença aqui é que, como a distância do fio pro ponto é , nós vamos pegar a fórmula da letra e, onde tiver , nós vamos colocar .
Além disso, na Fig. 2 vemos que , então vamos substituir esse cara também. Ok?
Assim, o campo será:
Agora vamos dar uma arrumada nesse cara.
Como os caras dentro da raíz estão divididos por 4, vamos tirar esse cara da raíz.
Ok... acho que agora não tem mais o que fazer. Vamos voltar ao problema.
Passo 3
De acordo com o problema:
Substituindo os caras que encontramos ali em cima:
Beleza, como temos que descobrir o valor de , vamos começar simplificando esses caras.
Dos dois lados nós temos no numerador e no denominador... então podemos sumir com esses caras.
Passo 4
Utilizando o resultado do item , calcule o módulo do campo magnético em em função de , e . A corrente deve circular na espira no sentido horário ou anti-horário para que o campo em tenha sentido saindo da página?
Na letra , vimos que o módulo do campo magnético gerado por um fio de comprimento no ponto , a uma distância do fio é dado por:
A diferença é que, de acordo com a Fig. 3, o comprimento do fio agora será e a distância do fio ao ponto será . Logo:
Po! Isso é semelhante ao raciocínio que tivemos na letra pra calcular , concorda?
Então, quando acabarmos de arrumar esse cara, ele tem que ficar assim:
Show! Só que como se tratam de 4 fios, o campo magnético resultando no ponto vai ser a soma dos campos magnéticos de cada fio, logo:
Resposta